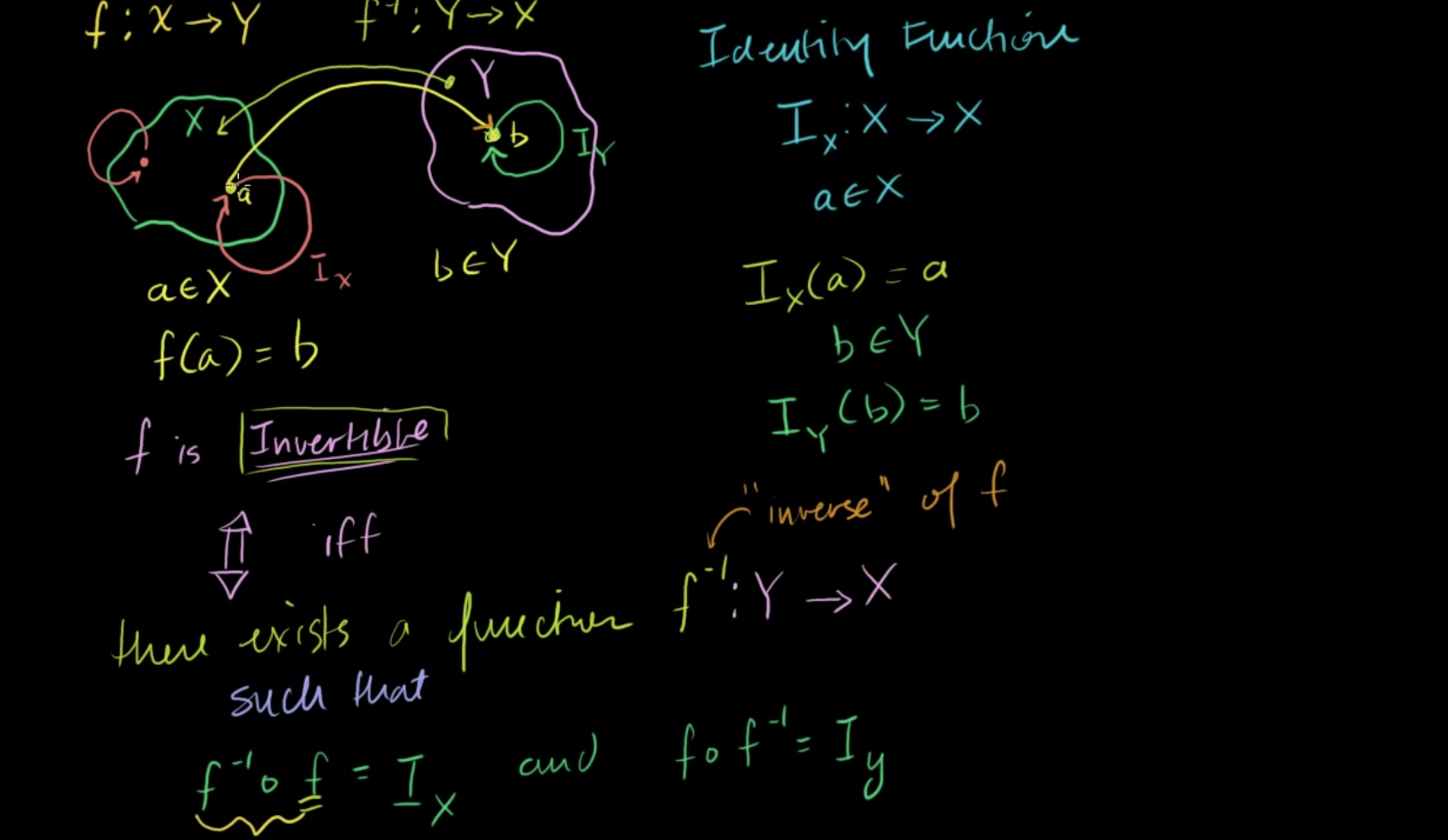SInce 20180106

(1) 가역성의 조건 앞에서 함수가 가역적이기 위해서는 두가지 조건을 만족해야만 한다고 했다. 단사함수이면서 전사함수이어야 한다는 것이었다. 함수 T가 Rn -> Rm으로 변환하는 함수라고할 때, T가 가역적인지 알아보는 법을 정리해보자. 함수 T는 선형변환이므로 T(x) = Ax로 표현할 수 있다. 전사함수가 되기 위해서는 A의 계수, Rank(A)가 m과 같아야 한다고 했다. 또한, 단사함수가 되기 위해서는 A의 계수, Rank(A)가 n과 같아야 한다고 했다. Rank(A) = m = n 이어야한다는 결론이 나온다. 즉, A는 정사각행렬이어야 한다는 조건이다. (n x n 행렬) 행렬 A는 a1, a2, ..., an으로 표현할 수 있고, 각 열벡터들은 n차원의 벡터들이다. 그리고, 계수가 열의 수..

(1) Ax = b의 해집합과 단사함수 10-3 글에서 변환이 가역성을 가지기 위해서는, 단사함수이면서 전사함수이어야 한다고 했다. 10-4에서는 변환이 전사함수가 되는 조건을 설명했다. ( Rank(A) = m 이면 전사함수 / 모든 열이 피벗변수 ) 10-5에서 Ax = b의 해집합이 Xh + Xp와 같이 표현된다고 했다. (Xp는 particular한 벡터, Xh는 N(A)) 그러므로 이번에는 x = Xh + Xp라는 해집합이 단사함수가 되는 조건에 대해서 알아보도록 하겠다. 변환 T는 X를 Y로 사상하고, T(x) = Ax라고 표현할 수 있다. A는 변환행렬이라고 가정했기 때문에, 변환 T는 A를 정의역 내의 벡터와 곱하는 것이라고 생각할 수 있다. 만약 T가 단사함수라면, 공역 Y의 어떤 b를 ..

(1) Ax = b에서 가능한 b의 집합 이번 글에서는 Ax = b에서 x의 해가 존재하도록 하는 b들의 집합을 구해보고, 해가 존재할 때 x가 어떤 형태의 집합인지 알아보는 것이 목적이다. (맨 밑 문단의 결론을 먼저 읽고 와서, 흐름을 따라가면 더 잘 이해가 될 수도?) R2에서 R2로 사상하는 선형변환 T가 있고, T = Ax 의 형태에서 A = [1 -3; -1 3]이라고 가정하자. [1 -3; -1 3] [x1, x2] = [b1, b2] 라고 해보면, 기약행사다리꼴 행렬의 형태로 나타낼 수 있다. rref = [1 -3 | b1 0 0 | b1 + b2] 전 글에서 말했듯이, 우항의 모든 값이 0인 행에서 좌항이 0이라면 해가 무수히 많고, 0이 아니라면 해가 존재하지 않는다고 했다. (전사함..

(1) 변환은 전사함수라는 것의 의미 변환 T가 Rn과 Rm을 대응한다고 할 때, 이 선형변환은 T(x) = Ax와 같은 행렬곱으로 나타낼 수 있다. 앞에서 변환이 가역성을 가지려면 두 가지 조건을 성립해야한다고 했다. 1) T는 전사함수이어야 한다. 2) T는 단사함수이어야 한다. 여기서는 T가 전사함수라는 것이 무슨 의미인지 알아보고자 한다. 이 글에서는 가역성을 정의하거나, 2번 조건을 다루지는 않을 것이다. 전사함수라는 것은 Rm의 모든 원소 b에 대해서 Ax = b인 최소 한 개의 해가 존재한다는 것이다. (x는 Rn의 원소) 여기서 A는 n개의 열벡터로 표현할 수 있고, (A = [a1, a2, ..., an] Ax = x1a1 + x2a2 + ... + xnan으로 표현할 수 있다. (A의 ..

(1) 가역성과 단사함수 / 전사함수의 관계 앞에서 가역성이 무엇을 의미하는지 알아봤다. 가역성이란 역함수라고 하는 다른 함수가 존재한다는 의미이며, 역함수와 원래 함수를 합성하면 항등함수가 된다. 즉, 공역의 모든 y에 대해 f(x) = y를 만족하는 유일한 해 x가 존재하는 경우에 가역성이 존재한다고 할 수 있다. 이 개념을 전사함수와 단사함수에 적용해보자. 유일한 해 x를 갖는다는 것은 y와 x가 일대일 대응이라는 것이며, 단사함수라는 뜻이다. 단사함수란 y값을 갖는 f(x)를 만족하는 x가 하나뿐이기 때문이다. 모든 y가 f(x)에 의해 사상된다는 것은 공역의 모든 원소가 치역이라는 의미이고, 이는 전사함수라는 뜻이다. 전사함수란 공역과 치역이 일치하는 함수이기 때문이다. 결론적으로, 가역성이 있..

(1) 전사함수(Surjective, onto) 전사함수(surjective, onto)라는 것은 공역에 있는 모든 원소가 치역에 있는 것이다. 그래서 수식적으로 표현하면, 공역의 모든 y에 대하여 최소한 하나의 x에 대해서 f(x) = y를 성립한다고 할 수 있다. 간단한 예로 X = [1, 2, 3, 4], Y = [A, B, C, D]가 있을 때, f(1) = A f(2) = B f(3) = C f(4) = D 라면, 모든 Y가 사상(mapping)되기 때문에 전사함수라고 할 수 있다. 만약, X에 5가 추가되어서 f(5) = D 라고 하더라도, 전사함수는 그대로 성립한다. 최소한 1개의 x가 y에 사상되는 것이기 때문에 여러 개의 x가 하나의 y에 대응되더라도 괜찮다. 하지만, Y에 E가 추가되었..

(1) 역함수의 정의 어떤 함수 f를 f : Χ -> Υ 라고 정의하고, f(^-1) : Y -> X라고 정의해보자. (역함수) a가 집합 X의 원소이고, b가 집합 Y의 원소일 때, f(a) = b 이고, f^-1(b) = a가 성립한다. 항등함수(대문자 Ι)란 Ι : X -> X 이고, I(a) = a가 되는 함수이다. 즉, 임의의 원소 a에 항등함수를 적용하면 결과값이 똑같이 a가 나온다는 것이다. 그림으로 표현해보면, 원과 같은 형태가 나오게 된다. 만약 f가 가역적(invertible)이라면, f(^-1)이 존재한다는 것과 필요충분조건이다. 필요충분조건이라는 것은 ( 또는 iff)로 나타낸다. (명제가 참이고, 역도 참이라는 뜻) "f의 역함수가 존재할 때, f는 가역적이다."라고 할 수 있다...

(1) 행렬곱 사실 행렬곱은 어려울 게 없다. 하지만 그냥 정리차원에서 하는 것이니, 슬쩍 읽어보면 끝일 듯하다. 행렬 A는 m x n 이고, 행렬 B는 n x k라고 하자. B를 열벡터의 형태로 표현하면 [b1, b2, ..., bk] 이다. AB를 해주면 A와 B의 열벡터의 곱으로 표현할 수 있고, [Ab1, Ab2, ..., Abn]이 된다. 실제 값을 대입해보자. A = [ 1 -1 2; 0 -2 1] , B = [1 0 1 1; 2 0 1 -1; 3 1 0 2;]라고 하자. AB를 A와 B의 열벡터의 곱으로 표현하면 위와 같이 된다. Ab1을 구할 때, a1과 b1의 내적으로 구하면 되고 풀어서 써보면 위와 같이 된다. 따라서, AB = 2 x 4의 행렬이 된다. A는 2 x 3 이고, 행렬 B..

(1) 선형변환이 합성되어도 선형변환일까? 선형변환이 합성되어도 여전히 선형변환인지 알아보자. 선형변환 S는 집합 X에서 집합 Y로 사상하는 변환으로, Rn을 Rm으로 사상한다. 선형변환 T는 집합 Y에서 집합 Z로 사상하는 변환으로, Rm을 Rl로 사상한다. 이를 그림으로 나타내보면, 위와 같이 그려볼 수 있다. T°S가 집합 X에서 Z로 사상하는 변환이라고 하면, T°S = T(S(x)) 라고 정의할 수 있다. 이 변환이 선형변환인지 알아보려면, 덧셈과 스칼라 곱에 닫혀있는지 확인해보면 된다. 1) 덧셈에 닫혀있나 T°S(x+y) = T(S(x+y))= T(S(x) + S(y)) -S는 선형변환이므로 덧셈에 닫혀있다= T(S(x)) + T(S(y)) - T는 선형변환이므로 덧셈에 닫혀있다 따라서, T..

(1) 단위벡터를 활용한 정사영 연산 간략화 이전 글에서 직선과 직선 위의 벡터 v, 임의의 벡터 x가 있을 때, 벡터 x를 정사영한 위치벡터를 구하는 방법을 알아봤다. 정사영 proj는 Rⁿ에서 Rⁿ으로 변환한다. proj(x) = {(x·v) / (v·v)} v v·v = ||v||² (자기 자신과의 내적은 길이의 제곱)으로 표현할 수 있기 때문에, proj(x) = {(x·v) / ||v||²} v 로 표현할 수도 있다. 길이가 1이라면 계산이 간단해지기 때문에, 길이가 1인 벡터(단위벡터)를 활용해서 정사영 계산을 좀 더 간단하게 해보자. 단위벡터를 구하는 방법은 벡터를 벡터의 길이로 나누면 된다. 예를 들면, v = [2 1] 이라면 길이인 √5로 나눈 [2/√5 1/√5]가 단위벡터 u가 된다..