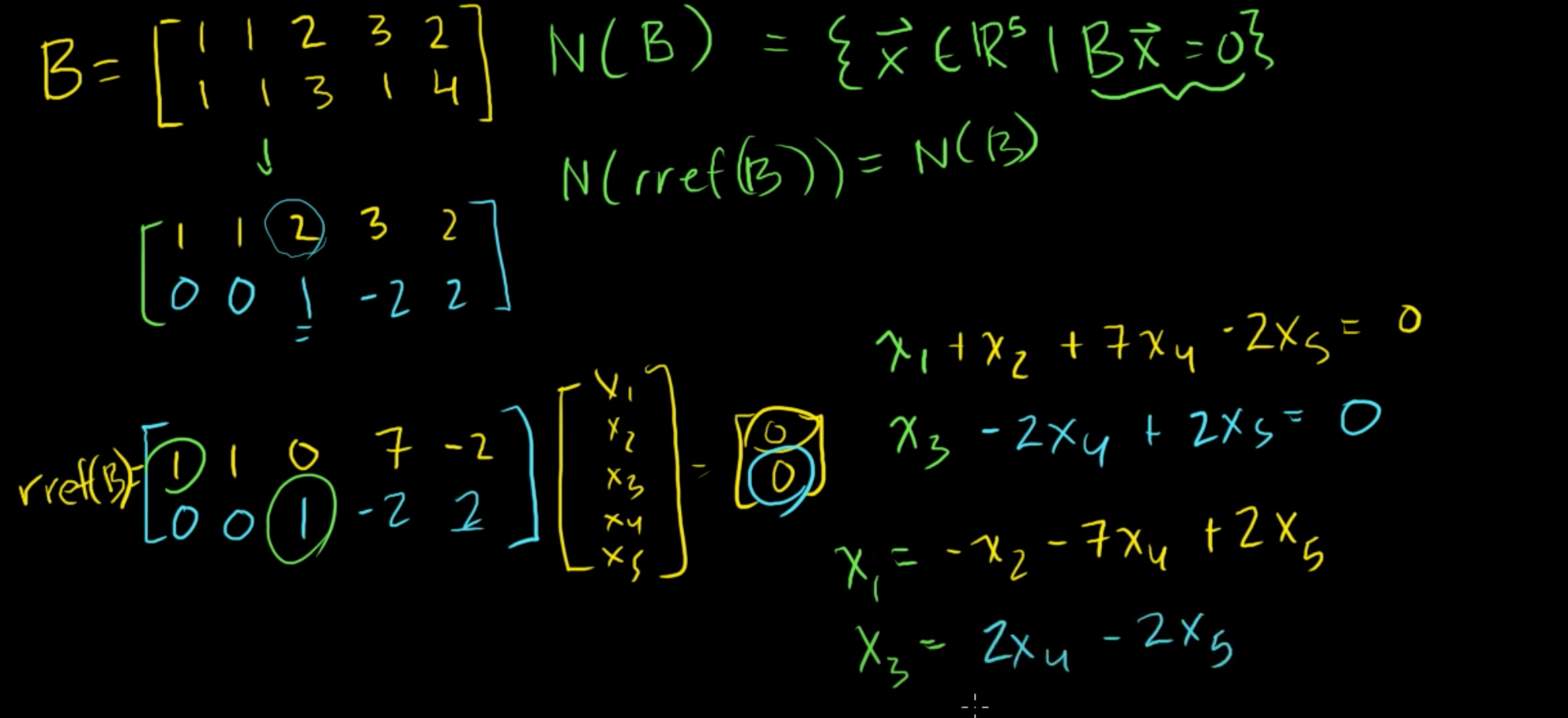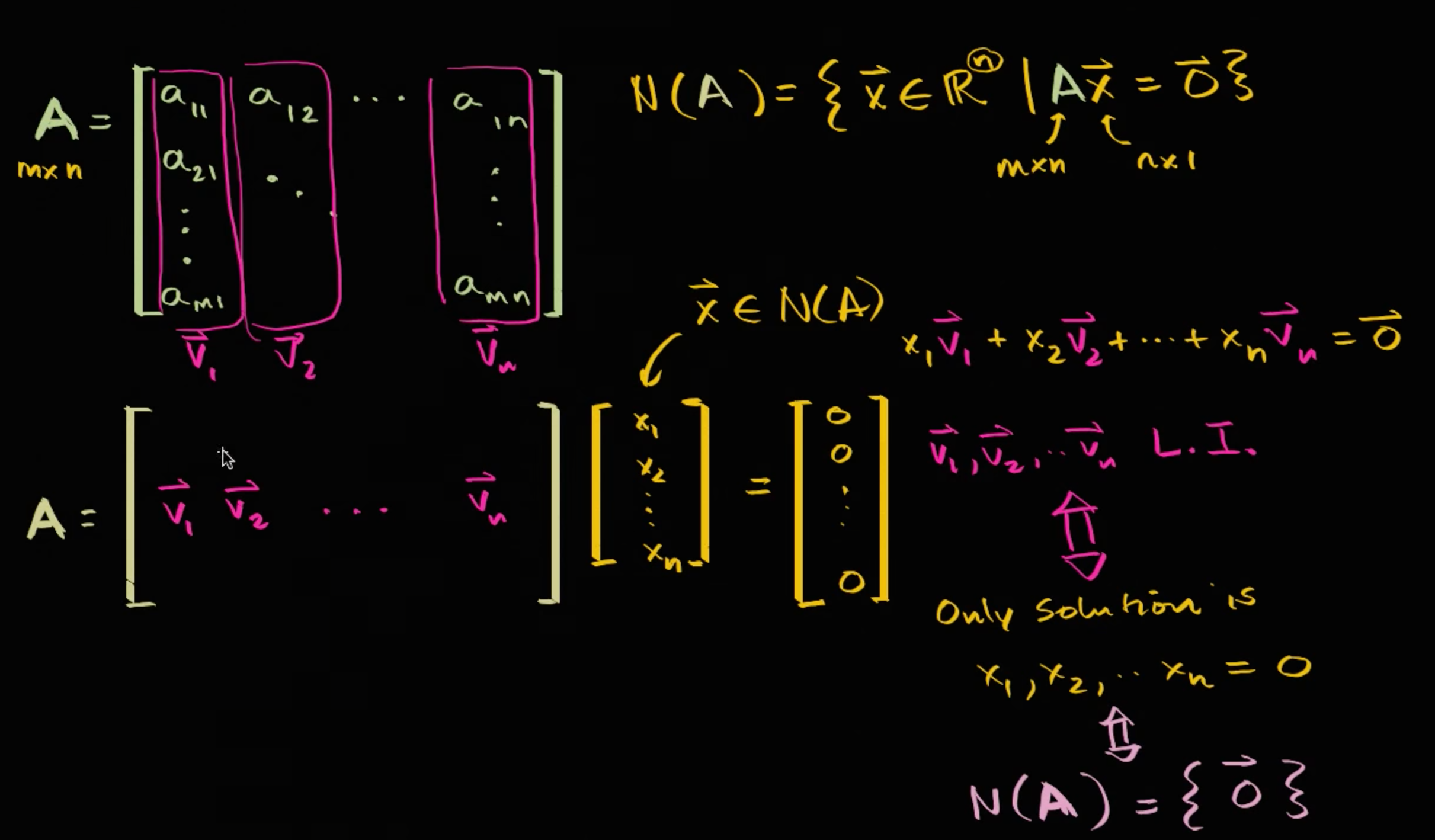SInce 20180106

(1) 고유벡터와 고유공간 앞의 예제에 이어서, 고유벡터와 고유공간을 구해보자. A = [1 2; 4 3]이었고, λ가 A의 고유값이라면 det(λIn - A) = 0의 필요충분조건이라고 했다. 그래서, λ = 5, -1 이라는 값을 앞에서 구해봤었다. Av = λv 이기 때문에, 0 = (λIn - A)v 가 성립하고, 어떠한 고유값 λ에 대해서 고유공간 Eλ = N(λIn - A) 와 같이 영공간의 형태로 표현할 수 있다. 즉, 고유공간은 영공간을 만드는 (λIn - A)가 된다. λ = 5 일 때, 영공간을 활용하여 고유공간을 구해보자. E5 = N([4 -2; -4 2]) [4 -2; -4 2]v = 0 이므로, 기약행사다리꼴 행렬을 활용하여 왼쪽 행렬을 간단하게 해보자. [4 -2; -4 2] ..

(1) 영공간의 직교보공간(직교여공간) 행렬 A가 있다. 이전 글에서 행공간은 열공간의 전치와 같다고 했다. 따라서, C(AT) = R(A)라고 할 수 있따. 그리고 C(AT)⊥ = N(A) 와 같다고 했다. 또한, C(A)⊥ = N(AT) (열공간의 직교여공간은 좌영공간과 같다) 14-5에서 다룬 것처럼 ⊥의 ⊥는 원래의 행렬로 돌아오기 때문에, 영공간의 직교여공간은 어떻게 될까? N(A)⊥ = (C(AT)⊥)⊥ = C(AT). 즉, A 영공간의 직교보공간은 A의 전치의 열공간과 같다. 좌영공간의 직교여공간은 어떻게 될까? N(AT)⊥ = (C(A)⊥)⊥ = C(A) 즉, A 좌영공간의 직교보공간은 A의 열공간과 같다. 정리하자면, N(A) = R(A)⊥ 이고, R(A) = N(A)⊥ 이다. N(AT)..

(1) 4대 부분공간의 직교 14장에서는 직교보공간(직교여공간)에 대해서 알아보려고 하는데, 이에 앞서서 앞에서 다룬 부분공간들이 어떻게 수직이 되는지 알아보고 넘어가려고 한다. 일단 내적이 0인 두 벡터는 수직이다. 그리고, 어떤 부분공간에 속한 모든 벡터들이 다른 부분공간에 속한 벡터들과 모두 수직이라면, 두 부분공간은 수직이다. 예를 들어, 행공간과 영공간은 수직이다. (2) 행공간과 영공간 행공간과 영공간은 직교이다. 행렬 A의 행공간은 A의 행 벡터로 생성되고, 영공간은 Ax = 0을 만족하는 x로 생성된다. Ax = 0는 [row1; row2; ....; row m) x = [0; 0; ...; 0]을 만족시키려면, row1*x1 = 0 이 되므로, 모든 행 벡터와 x의 내적이 0이 되어야한다..

(1) 영공간의 차원 이번 내용은 어려울 게 없다. 그냥 앞의 내용을 다시 정리하고, 이를 기반으로 몇 가지 새로운 사실을 뽑아낸다고 생각하면 된다. 행렬 B [1 1 2 3 2; 1 1 3 1 4;]가 있고, 이 행렬 B의 영공간을 구해보자. B의 영공간은 Bx = 0을 만족하는 5차원 벡터 x의 집합이고, 기약행사다리꼴행렬의 영공간과 동일하다고 했다. 따라서, 기약행사다리꼴행렬을 구해보면, [1 1 0 7 -2; 0 0 1 -2 2]가 된다. 여기서 첫째 줄의 x1과 둘째 줄의 x3이 피벗변수이다. x2 역시 피벗변수가 될 수는 있지만, 식을 2개밖에 못 구하기 때문에 x1을 피벗변수로 설정했다. 피벗 변수에 대한 연립방정식을 세우고, 피벗 변수에 대한 식으로 다시 정리해보자. x1 = -x2 - 7..

(1) 열공간의 기저 이번에는 행렬, 영공간, 열공간, 선형독립을 결합해서 다뤄보도록 하겠다. 행렬 A가 있고, 이 행렬의 열공간과 영공간의 기저에 대해서 알아보자. (기저란 부분공간을 생성하는 선형독립한 벡터의 집합이다.) A의 열공간은 span(열벡터)라고 할 수 있고, (연보라) A의 영공간은 기약행사다리꼴의 영공간과 동일하다. (하늘색) 그리고, 만약 영공간이 영벡터만을 가진다면 A의 열벡터들은 선형독립이라고 했다. 그래서 우리는 열벡터가 선형독립인지 알기 위해 A의 영공간을 구하여 판별해보도록 하겠다. 기약행사다리꼴 형태의 행렬 A를 구하면, (초록색) [ 1 0 3 2 ; 0 1 -2 -1 ; 0 0 0 0] 이 된다. Ax = 0을 성립하는 x의 집합이 영공간이고, A의 영공간과 기약행사다리..

(1) 영공간과 선형독립 m개의 행과 n개의 열로 이루어져 있는 행렬 A가 있다. 이번에는 A의 열벡터의 선형독립과 선형종속을 A의 영공간과 연관지어 보겠다. A에는 n개의 열이 있고, 각 열은 m차원의 벡터로 이뤄져있다. A의 각 열을 v1, v2, ..., vn이라고 할 수 있다. 그러면 m×n인 행렬 A를 열벡터들의 행렬로 바꿔 쓸 수 있다. A의 영공간이 뭔지 다시 적어보면, 영공간은 n차원 공간의 벡터 중에서 Ax = 0을 만드는 x벡터의 집합을 말한다. 그러므로 열벡터로 표현한 행렬 A를 어떠한 벡터 x와 곱하면, m개의 0을 갖는 영벡터가 나오게 될 것이다. 행렬의 곱을 풀어주면, x1v1+x2v2+...+xnvn=0 이 된다. 이 식은 선형독립에서 봤던 식과 동일하다. x1v1+x2v2+...

(1) 영공간 계산해서 구하기 지난번에 영공간의 이론적인 의미로 영공간이 하나의 부분공간이라는 걸 증명했다. 간략하게 앞 내용을 정리하면, 영공간은 행렬과 곱했을 때 영벡터가 나오는 모든 벡터의 집합이다. 이번에는 영공간을 구해보겠다. 위와 같이 3x4 행렬 A [1 1 1 1; 1 2 3 4; 4 3 2 1]가 있고, A에 곱해서 영벡터를 만드는 벡터 x가 있다고 하자. 벡터 x는 [x1, x2, x3, x4]이고, R4에 속해있는 벡터이다. 따라서, N(A)는 R4에 속해있으면서, Ax = 영벡터를 성립하는 벡터들의 집합이다. (N은 Null Space의 N을 의미함) Ax = 영벡터 라는 식을 풀어보자. 1 × x1 + 1 × x2 + 1 × x3 + 1 × x4 = 0 1 × x1 + 2 × x2..

(1) 영공간(Null Space)의 정의 영공간에 대해서 정리하기 전에 부분공간에 대한 개념을 복습하고 넘어가자. s는 3가지 조건을 만족시켜야만 부분 공간이라고 할 수 있다. 1) 영벡터는 s의 원소이다. 2) 만약 v1과 v2가 부분공간의 원소라면 v1+v2 또한 부분공간의 원소이다. 즉, 부분공간은 덧셈에 대해 닫혀있다 3) 부분공간은 곱셈에 대해서도 닫혀있다. 실수 스칼라c를 부분공간의 원소 v1에 곱한다면 그 값도 부분공간의 원소가 된다. 그렇다면, m × n인 행렬 A가 있고, 벡터 x를 곱했을 때 영벡터가 되는 동차방정식을 세워보자. 행렬 A가 n개의 열을 가지고 있으므로, x는 n개의 성분을 가지는 Rⁿ의 원소이다. 행렬 A와 벡터 x의 곱이 영벡터를 만족하는, Rⁿ의 원소인 모든 벡터 ..