(1) 선형변환이 합성되어도 선형변환일까?
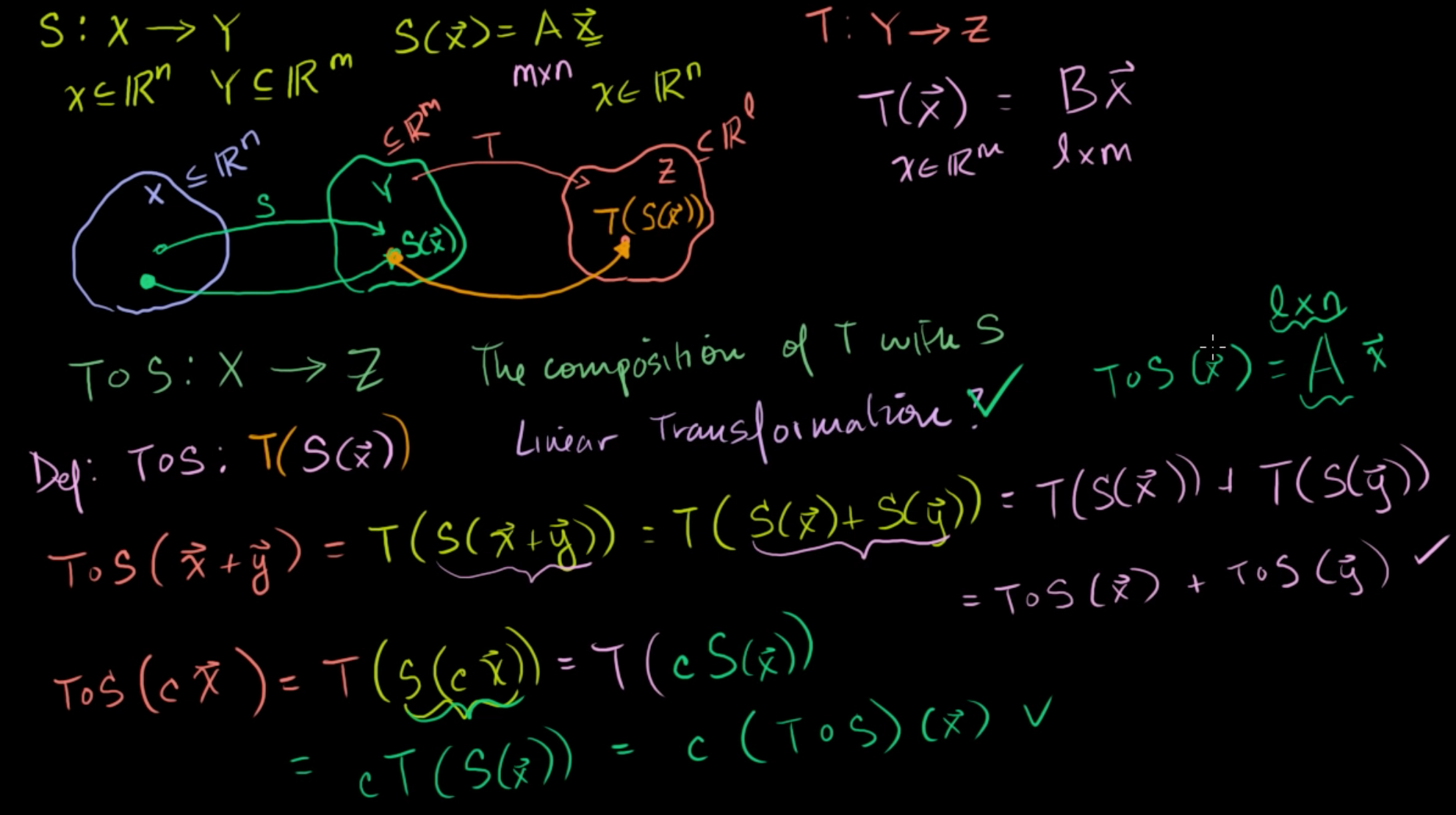
선형변환이 합성되어도 여전히 선형변환인지 알아보자.
선형변환 S는 집합 X에서 집합 Y로 사상하는 변환으로, Rn을 Rm으로 사상한다.
선형변환 T는 집합 Y에서 집합 Z로 사상하는 변환으로, Rm을 Rl로 사상한다.
이를 그림으로 나타내보면, 위와 같이 그려볼 수 있다.
T°S가 집합 X에서 Z로 사상하는 변환이라고 하면, T°S = T(S(x)) 라고 정의할 수 있다.
이 변환이 선형변환인지 알아보려면, 덧셈과 스칼라 곱에 닫혀있는지 확인해보면 된다.
1) 덧셈에 닫혀있나
T°S(x+y) = T(S(x+y))= T(S(x) + S(y)) -S는 선형변환이므로 덧셈에 닫혀있다= T(S(x)) + T(S(y)) - T는 선형변환이므로 덧셈에 닫혀있다
따라서, T°S는 덧셈에 닫혀있다.
2) 스칼라 곱에 닫혀있나
T°S(cx)
= T(S(cx))
= T(cS(x)) - S는 선형변환
= cT(S(x)) - T는 선형변환
따라서, 스칼라 곱에 닫혀있다.
결론적으로 선형변환의 합성은 선형변환이다.
이 말은 즉 T와 S의 합성은 행렬벡터의 곱 형태로 쓸 수 있다는 말이다.
T°S(x) = Ax 라고 할 때, T°S는 Rn을 Rl으로 사상하고 A는 l x n 의 행렬이다.
(2) 합성 선형변환 행렬 구하기

T(x) = Bx (B는 l x m 행렬)
S(x) = Ax (A는 m x n 행렬) 이고,
T°S(x)
= T(S(x))
= T(Ax)
= B(Ax)
처럼 표현할 수 있다.
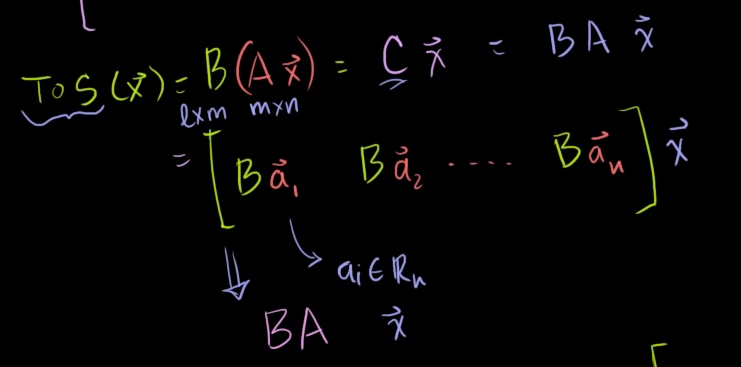
그러면 이와 같이 B와 A의 열벡터의 곱으로 바꿔서 표현할 수 있다.
B(Ax)
= [Ba1 Ba2 ... Ban]x
= BAx
따라서, T°S(x) = Cx 와 같이 선형변환의 형태로 표현할 수 있고, C는 BA의 값과 같다.
사실 특별할 내용은 없다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 10-1. 역함수란? (0) | 2023.04.02 |
|---|---|
| 9-2. 행렬곱 (0) | 2023.04.01 |
| 8-6. 행렬벡터 곱으로 정사영 표현하기 (0) | 2023.03.30 |
| 8-5. 정사영(Projection) (0) | 2023.03.29 |
| 8-4. 단위벡터(Unit Vector) (0) | 2023.03.28 |