(1) 단위벡터를 활용한 정사영 연산 간략화

이전 글에서 직선과 직선 위의 벡터 v, 임의의 벡터 x가 있을 때, 벡터 x를 정사영한 위치벡터를 구하는 방법을 알아봤다.
정사영 proj는 Rⁿ에서 Rⁿ으로 변환한다.
proj(x) = {(x·v) / (v·v)} v
v·v = ||v||² (자기 자신과의 내적은 길이의 제곱)으로 표현할 수 있기 때문에,
proj(x) = {(x·v) / ||v||²} v 로 표현할 수도 있다.
길이가 1이라면 계산이 간단해지기 때문에, 길이가 1인 벡터(단위벡터)를 활용해서 정사영 계산을 좀 더 간단하게 해보자.
단위벡터를 구하는 방법은 벡터를 벡터의 길이로 나누면 된다.
예를 들면, v = [2 1] 이라면 길이인 √5로 나눈 [2/√5 1/√5]가 단위벡터 u가 된다.
proj(x)
= {(x·u) / ||u||²} u
= (x·u) u
처럼 간단하게 표현할 수 있다.
(2) 정사영은 선형변환인가?

projection은 선형변환일까?
덧셈에 닫혀있는지와 스칼라곱에 닫혀있는지 알아보면 알 수 있다.
1. 덧셈
proj(a+b)
= ((a+b) · u) u
= (a·u + b·u) u
= (a·u)u + (b·u)u
= proj(a) + proj(b)
벡터의 합의 투영과 벡터의 투영의 합이 같다. 따라서, 닫혀있다.
2. 스칼라 곱
proj(ca)
= (ca · u) u
= c(a · u) u
= c proj(a)
벡터의 곱의 투영이 벡터의 투영의 곱과 같다. 따라서, 닫혀있다.
투영이 선형변환이라는 것은 proj(x) = Ax 와 같이 행렬변환으로 표현할 수 있다는 뜻이다.
(3) 정사영의 행렬변환 표현

앞에서 정사영이 Ax와 같은 형태로 표현될 수 있다고 했다.
따라서, proj(x) = Ax = (x·u) u 이다.
A를 구한다면 쉽게 투영할 수 있다.
n차원에 대해서 할 수도 있지만, 간단하게 proj가 R² -> R² 일 때를 가정하고 A를 구해보자.
u = [u1, u2] (투영될 직선 위에 존재하는 벡터의 단위행렬)
A는 단위행렬의 열에 변환을 적용한 형태로 바꿔서 표현할 수 있다.
x = [1 0; 0 1] [x1 x2] 의 형태로 표현할 수 있기 때문에,
Ax = (x·u) u = [ ([1 0]·u) u, ([0 1]·u) u ] [x1 x2]= [ u1 u, u2 u] [x1 x2]= [ u1 [u1 u2], u2 [u1 u2] ] [x1 x2]= [ u1² u2u1; u1 u2 u2²] [x1 x2]
A = [ u1² u2u1; u1 u2 u2²]
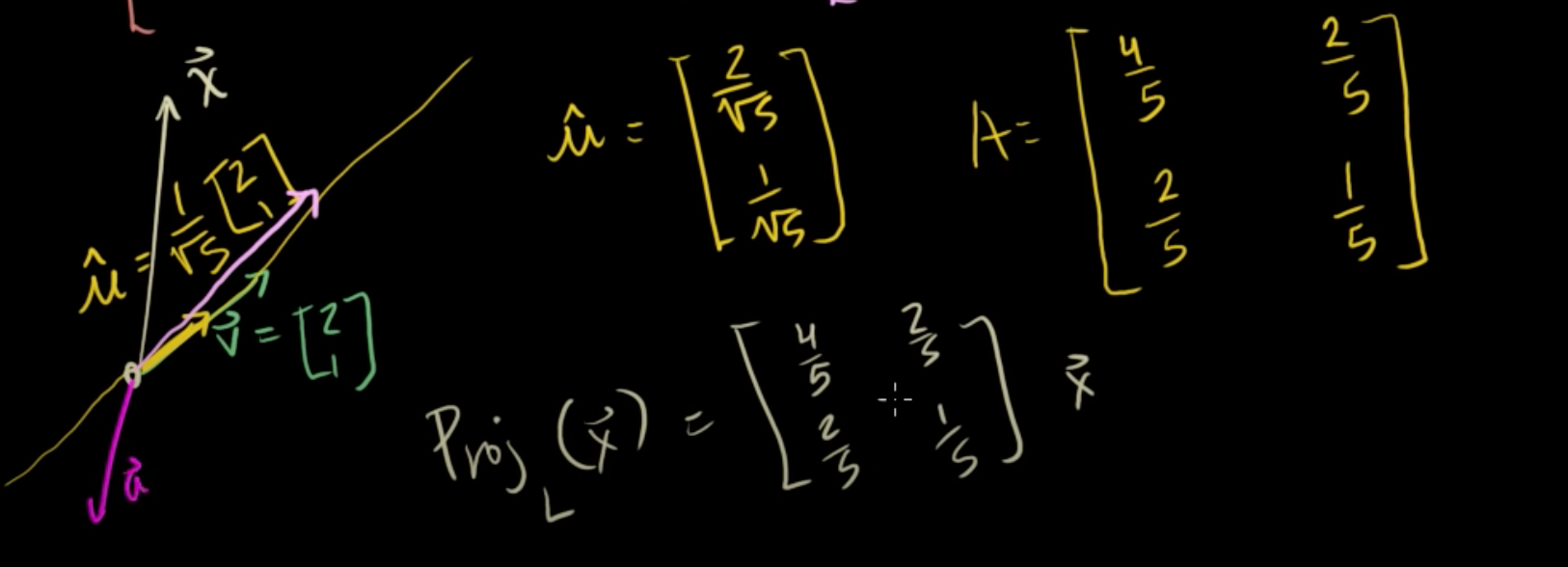
실제 예시를 들어보자.
v = [2 1]
x = [x1 x2] 이라면,
u = [2/√5 1/√5]
A = [4/5 2/5 ; 2/5 1/5]
x가 v를 포함하는 원점을 지나는 직선 L에 투영되면, [4/5 2/5 ; 2/5 1/5]x 가 된다.
*** 만약에 L이 원점을 안 지난다면, 선형변환이 되지 않기 때문에 이 같은 연산은 성립하지 않는다.
행렬벡터의 곱으로 표현하니, 투영의 연산이 엄청나게 빨라졌다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 9-2. 행렬곱 (0) | 2023.04.01 |
|---|---|
| 9-1. 선형변환의 합성(1) (0) | 2023.04.01 |
| 8-5. 정사영(Projection) (0) | 2023.03.29 |
| 8-4. 단위벡터(Unit Vector) (0) | 2023.03.28 |
| 8-3. 선형변환(R3에서의 회전) (0) | 2023.03.27 |