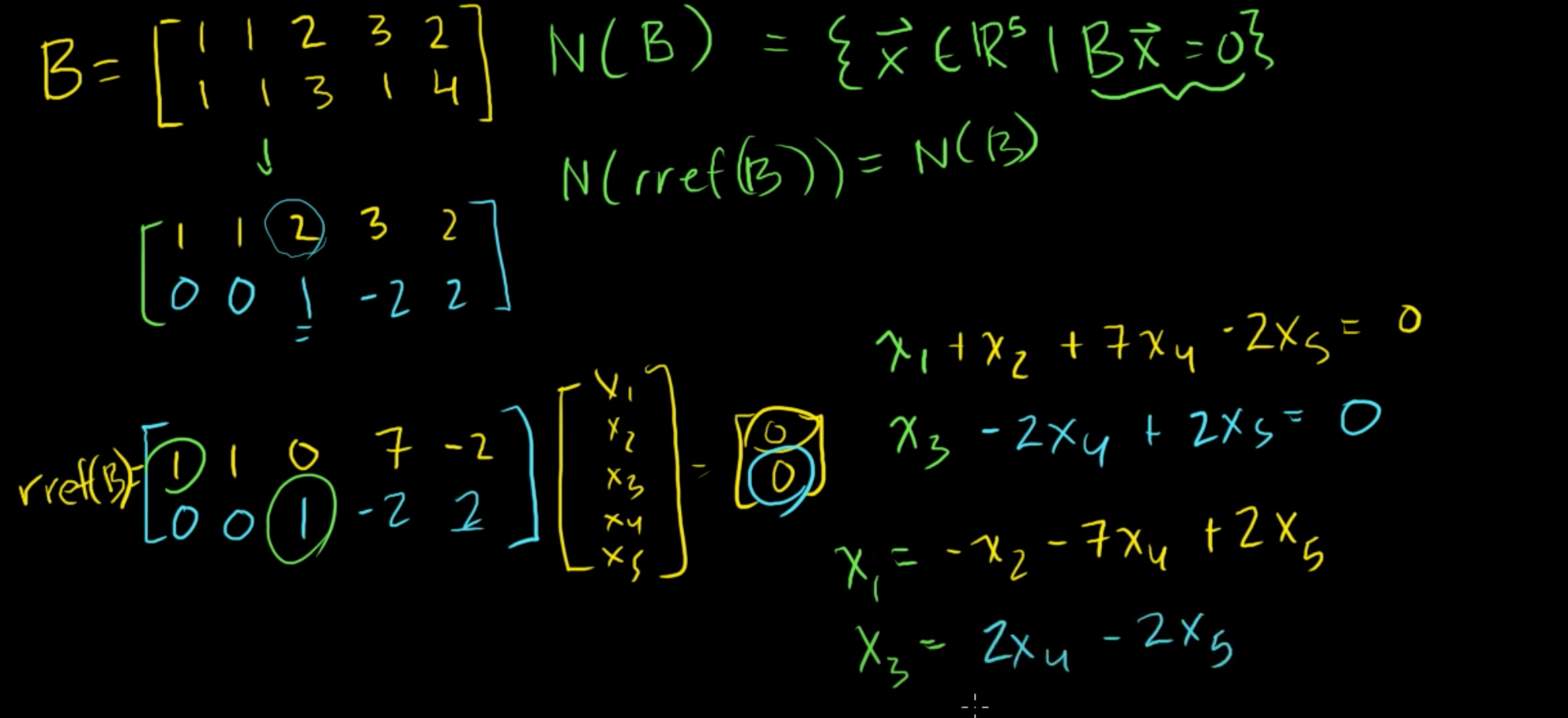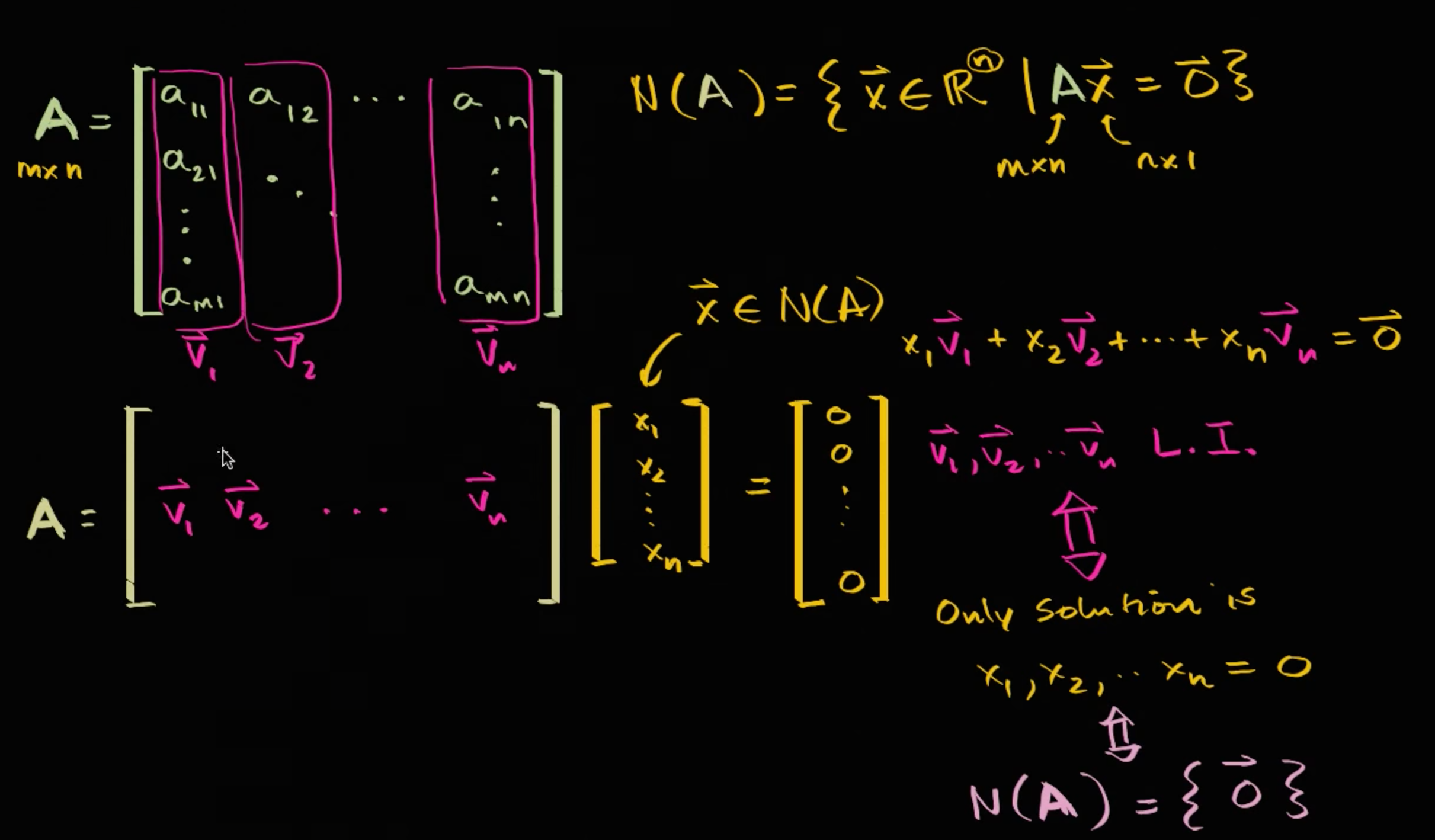SInce 20180106

(1) 행렬과 벡터의 곱, 그리고 선형 변환 행렬을 벡터와의 내적으로 변환하는 과정을 보여주고, 이런 변환이 선형변환인지 알아보도록 하자. m x n 행렬 A는 열벡터 v1, v2부터 vn으로 표현할 수 있다. 이 때, 변환 T는 Rn에서 Rm으로 가는 변환이라고 하고, 벡터 x가 입력되면 행렬 A를 내적하여 나온 값으로 변환해준다고 해보자. 조금 생소해보일 수도 있지만, 이 역시 변환의 일종이니 익숙해지도록 노력해보자. T(x) = Ax 이고, 결과는 Rm 상에 존재한다. Ax = [v1, v2, ..., vn] [x1; x2; ... xn] 이라는 행렬과 벡터의 내적으로 표현할 수 있고, 이를 풀어보면, v1x1 + v2x2 + .. + vnxn 이다. 이 결과는 Rm 상에 존재하며, v1, v2, ..

(1) 선형변환 (Linear Transformation) 함수는 쉽게 말하면 하나의 값을 다른 값으로 변환해주는 식이다. 변환에서도 특별한 종류인 선형변환에 대해 알아보겠다. 선형변환은 Rn에서 Rm으로 변환해주는 것이고, 무엇인가가 선형변환이라는 것은 필요충분조건 2가지를 만족한다는 것이다. 조건 1) 두 벡터의 합 벡터의 변환 결과는 벡터 각각을 선형변환하여 더한 것과 같다. 조건 2) 벡터에 스칼라나 실수를 곱한 것을 변환한 결과는 벡터를 변환한 것에 스칼라배한 것과 같다. 이러한 규칙으로 선형변환인지 아닌지 판별할 수 있는지 알아보자. 변환 T는 (x₁, x₂)를 (x₁+x₂, 3x₁)으로 바꿔주는 함수가 있다고 가정하자. (R²에서 R²로 변환) T가 선형변환인지 아닌지 판단해보자. 조건 1)..

(1) 행렬 A의 기저열과 나머지 열의 관계 6-9 글에서 A의 열공간에 대한 기저를 찾는 방법을 정리했다. 그리고 6-10에서는 기약행사다리꼴의 피봇 열이 기저이고, 이에 대응하는 A의 열 역시 기저라는 사실을 보였다. 이번에는 A의 기저 열 외의 열들이 왜 기저가 아니고, 기저 열들의 선형결합으로 나타낼 수 있는지 알아보겠다. 행렬 A와 A의 기약행사다리꼴행렬 R이 있으며, r1, r2, r4는 선형독립이면서 기저이고, 이에 대응하는 a1, a2, a4도 선형독립이면서 열벡터를 생성하는 기저이다. (왜냐하면 R과 A가 같은 영공간을 갖기 때문이다.) 기저 열만으로 이뤄진 span(a1, a2, a4)는 C(A)이고, 기저 열과 다른 열벡터로 이뤄진 span(a1, a2, a3, a4, a5) 역시 C..

(1) 기약행사다리꼴 행렬의 열 지난번에 기약행사다리꼴의 피벗 열이 기존 행렬의 열공간에 대한 기저라고 했다. 위의 경우에는 열공간의 계수, 차원이 3이다. 그런데 왜 기약행사다리꼴의 피벗 열이 A의 열공간에 대한 기저 열이 되는 걸까? 그 이유를 알아보도록 하자. 행렬 A가 있고, A의 기약행사다리꼴 행렬 R이 있다. R에서 r1, r2, r4는 피벗 열이고, 선형독립이다. 왜냐하면 다른 열의 0을 이용하여 1을 구할 수 없기 때문이다. 이들은 선형독립이기 때문에, c1r1 + c2r2 + c4r4 = 0 에서 방정식의 해는 유일하다. c1 = c2 = c4 = 0 가 유일한 해이다. Rx = 0 이라는 영공간을 구하려면, c3, c5가 0이어야만 한다. R의 영공간은 A의 영공간과 동일하기 때문에, ..

(1) 열공간의 차원(랭크) 이전에는 행렬의 열공간은 생각보다 구하기 단순하다는 것을 볼 수 있었다. A의 열공간은 A의 열벡터들의 선형결합식과 같고, 열벡터들의 생성이다. 그래서 우선 열벡터들을 각각 a1, a2, a3, a4, a5로 불러보자. 그러면 A의 열공간은 span(a1, a2, a3, a4, a5)과 같다고 할 수 있다. 우리가 이번에 알고 싶은 것은 열벡터들이 열공간의 기저가 되는지이다. A의 열벡터의 기저 = C(A)를 생성하는 벡터 이다. 기저 벡터들은 모두 선형독립이여야 한다. 그래서 우선은 A를 기약행사다리꼴로 만들어서, 피벗벡터와 자유벡터를 구해보자. 기약행사다리꼴 R은 [1, 0, -1, 0, 4 0, 1, 2, 0, 1 0, 0, 0, 1, -3 0, 0, 0, 0, 0] 이..

(1) 영공간의 차원 이번 내용은 어려울 게 없다. 그냥 앞의 내용을 다시 정리하고, 이를 기반으로 몇 가지 새로운 사실을 뽑아낸다고 생각하면 된다. 행렬 B [1 1 2 3 2; 1 1 3 1 4;]가 있고, 이 행렬 B의 영공간을 구해보자. B의 영공간은 Bx = 0을 만족하는 5차원 벡터 x의 집합이고, 기약행사다리꼴행렬의 영공간과 동일하다고 했다. 따라서, 기약행사다리꼴행렬을 구해보면, [1 1 0 7 -2; 0 0 1 -2 2]가 된다. 여기서 첫째 줄의 x1과 둘째 줄의 x3이 피벗변수이다. x2 역시 피벗변수가 될 수는 있지만, 식을 2개밖에 못 구하기 때문에 x1을 피벗변수로 설정했다. 피벗 변수에 대한 연립방정식을 세우고, 피벗 변수에 대한 식으로 다시 정리해보자. x1 = -x2 - 7..

(1) 열공간의 생성과 방정식 앞에서 사용했던 식을 그대로 가져왔다. 행렬 A는 다음과 같다. [ 1 1 1 1; 2 1 4 3; 3 4 1 2;] {[1 2 3]과 [1 1 4]}는 A의 열공간의 기저라고 했고, {[1 2 3], [1 1 4]}의 생성은 A의 열공간을 나타낸다. x, y, z 축을 R3평면에 그려서, 3D 공간을 나타내자. [1, 2, 3] 벡터를 표현하면 노란색, [1, 1, 4] 벡터를 표현하면 주황색이라고 할 수 있다. 그리고 열 공간은 이 두 벡터(기저)의 생성(선형결합)과 같으며, 선형결합식들은 핑크색 평면을 이룬다. 평면위의 위치벡터 x를 보라색으로 표현했다. 이 때의 핑크색 열공간의 방정식을 구해보는게 이번 글의 목적이다. R3에서 열공간의 식(평면의 식)을 구하는 방법은..

(1) 열공간의 기저 이번에는 행렬, 영공간, 열공간, 선형독립을 결합해서 다뤄보도록 하겠다. 행렬 A가 있고, 이 행렬의 열공간과 영공간의 기저에 대해서 알아보자. (기저란 부분공간을 생성하는 선형독립한 벡터의 집합이다.) A의 열공간은 span(열벡터)라고 할 수 있고, (연보라) A의 영공간은 기약행사다리꼴의 영공간과 동일하다. (하늘색) 그리고, 만약 영공간이 영벡터만을 가진다면 A의 열벡터들은 선형독립이라고 했다. 그래서 우리는 열벡터가 선형독립인지 알기 위해 A의 영공간을 구하여 판별해보도록 하겠다. 기약행사다리꼴 형태의 행렬 A를 구하면, (초록색) [ 1 0 3 2 ; 0 1 -2 -1 ; 0 0 0 0] 이 된다. Ax = 0을 성립하는 x의 집합이 영공간이고, A의 영공간과 기약행사다리..

(1) 열공간 정의 앞에서는 영공간에 대해서 적었는데, 이제는 열공간에 대해서 적어보려고 한다. 일단 mxn의 행렬 A를 정의해보자. A는 [v1 v2 ... vn]과 같이 열벡터의 모음으로 다시 써볼 수 있다. 이 때, 열벡터는 n개만큼 있고, 각각의 열벡터는 m개의 성분을 가지는 m차원 공간의 원소이다. 열공간은 이 열벡터들의 모든 가능한 선형결합이라고 정의할 수 있다. 다시 말해 A의 열공간은 n개의 열벡터들로 가능한 모든 선형결합의 집합이라고 할 수 있다. 선형결합은 다른 말로 말하면 생성(Span)이기 때문에, A의 열공간(C(A))은 span(v1, v2, ... , vn)이 된다. 열공간이 부분공간인지 알아보자. 조건1) 0벡터를 포함하는가? (연두색) A의 열공간의 원소인 벡터 a가 있다고..

(1) 영공간과 선형독립 m개의 행과 n개의 열로 이루어져 있는 행렬 A가 있다. 이번에는 A의 열벡터의 선형독립과 선형종속을 A의 영공간과 연관지어 보겠다. A에는 n개의 열이 있고, 각 열은 m차원의 벡터로 이뤄져있다. A의 각 열을 v1, v2, ..., vn이라고 할 수 있다. 그러면 m×n인 행렬 A를 열벡터들의 행렬로 바꿔 쓸 수 있다. A의 영공간이 뭔지 다시 적어보면, 영공간은 n차원 공간의 벡터 중에서 Ax = 0을 만드는 x벡터의 집합을 말한다. 그러므로 열벡터로 표현한 행렬 A를 어떠한 벡터 x와 곱하면, m개의 0을 갖는 영벡터가 나오게 될 것이다. 행렬의 곱을 풀어주면, x1v1+x2v2+...+xnvn=0 이 된다. 이 식은 선형독립에서 봤던 식과 동일하다. x1v1+x2v2+...