반응형
(1) 기약행사다리꼴 행렬의 열
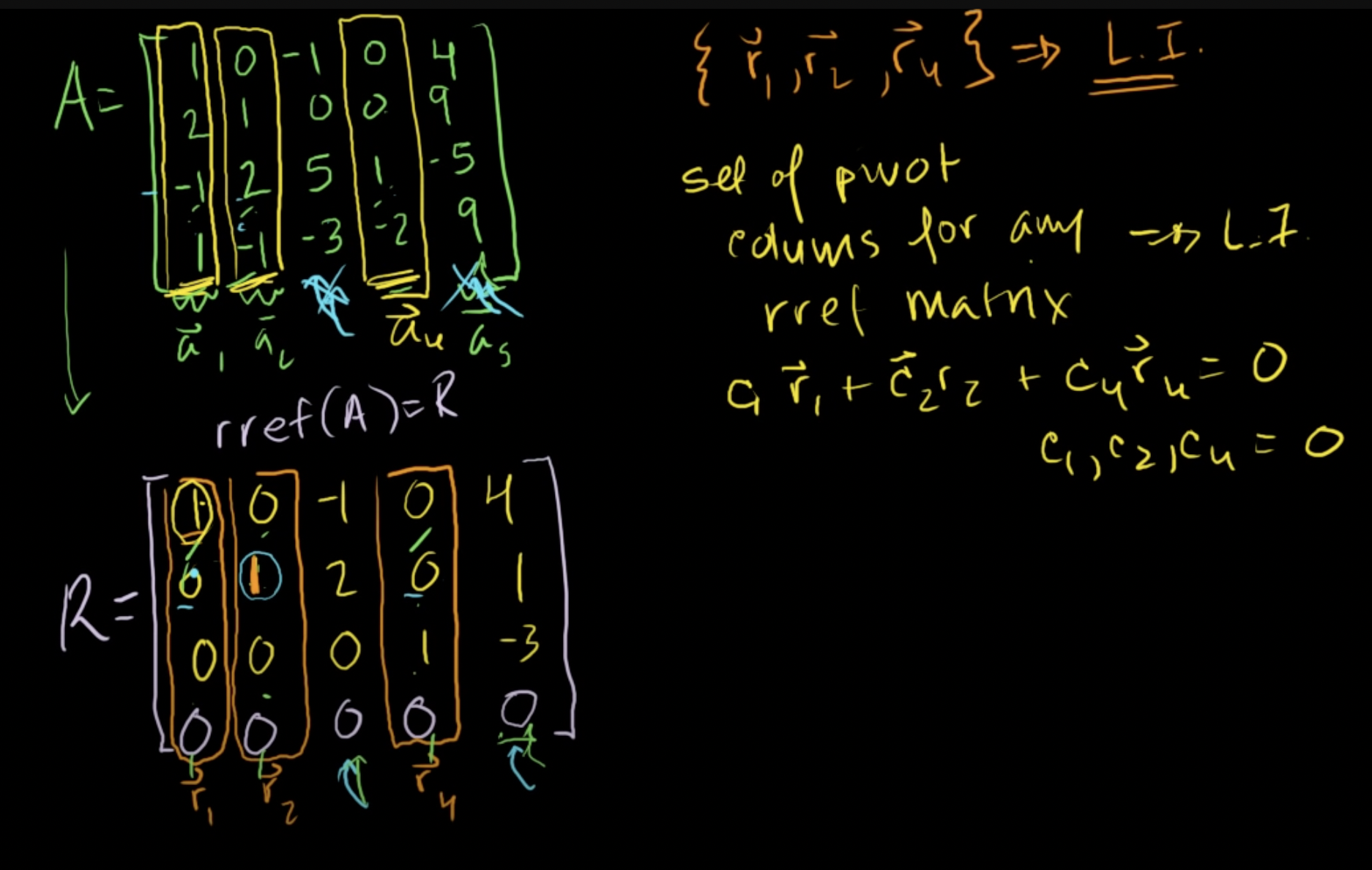
지난번에 기약행사다리꼴의 피벗 열이 기존 행렬의 열공간에 대한 기저라고 했다.
위의 경우에는 열공간의 계수, 차원이 3이다.
그런데 왜 기약행사다리꼴의 피벗 열이 A의 열공간에 대한 기저 열이 되는 걸까?
그 이유를 알아보도록 하자.
행렬 A가 있고, A의 기약행사다리꼴 행렬 R이 있다.
R에서 r1, r2, r4는 피벗 열이고, 선형독립이다.
왜냐하면 다른 열의 0을 이용하여 1을 구할 수 없기 때문이다.
이들은 선형독립이기 때문에, c1r1 + c2r2 + c4r4 = 0 에서 방정식의 해는 유일하다.
c1 = c2 = c4 = 0 가 유일한 해이다.
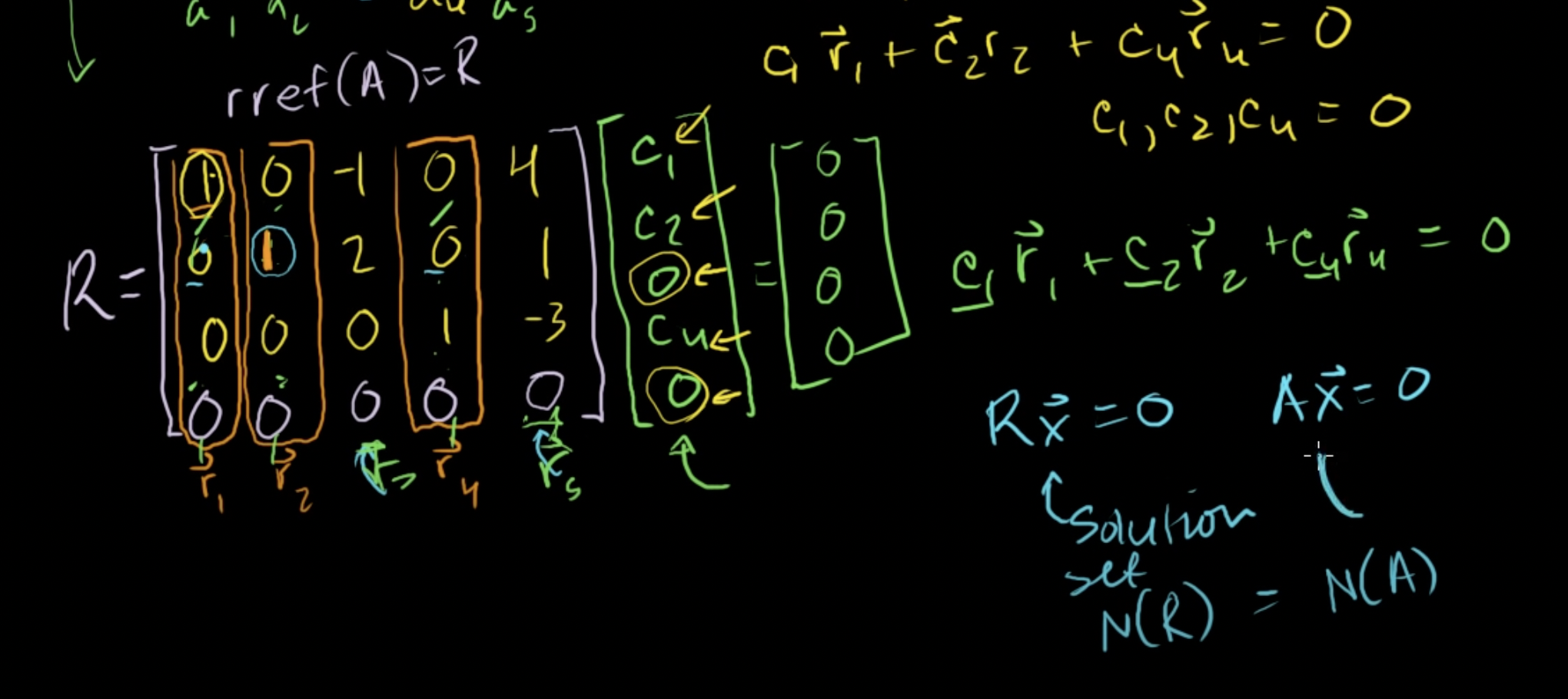
Rx = 0 이라는 영공간을 구하려면, c3, c5가 0이어야만 한다.
R의 영공간은 A의 영공간과 동일하기 때문에, A의 해가 [c1, c2, 0, c4, 0]이 된다.

따라서, Ax = 0 을 만족하는 해집합 [c1, c2, 0, c4, 0]를 대입해보면
c1a1 + c2a2 + c4a4 = 0 이 된다.
이 식의 해는 c1 = c2 = c4 = 0 이 유일하며,
a1, a2, a4는 선형독립이라는 사실을 도출해낼 수 있다.
6-9. 열공간의 차원(랭크)에서
R의 피벗 열들은 선형독립이기 때문에, r1, r2, r4는 선형독립이다.
따라서, 이에 대응하는 A의 열들 a1, a2, a4 또한 선형독립한다.
라고 하고 그냥 넘어갔는데, 영공간을 이용해서 연결한 결과이다.
반응형
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 7-1. 선형변환과 필요충분조건 (0) | 2023.03.15 |
|---|---|
| 6-11. 후보기저의 열공간 생성 (1) | 2023.03.14 |
| 6-9. 열공간의 차원(랭크) (0) | 2023.03.11 |
| 6-8. 영공간의 차원 (0) | 2023.03.10 |
| 6-7. 열공간의 생성과 방정식 (0) | 2023.03.09 |