(1) 영공간의 차원
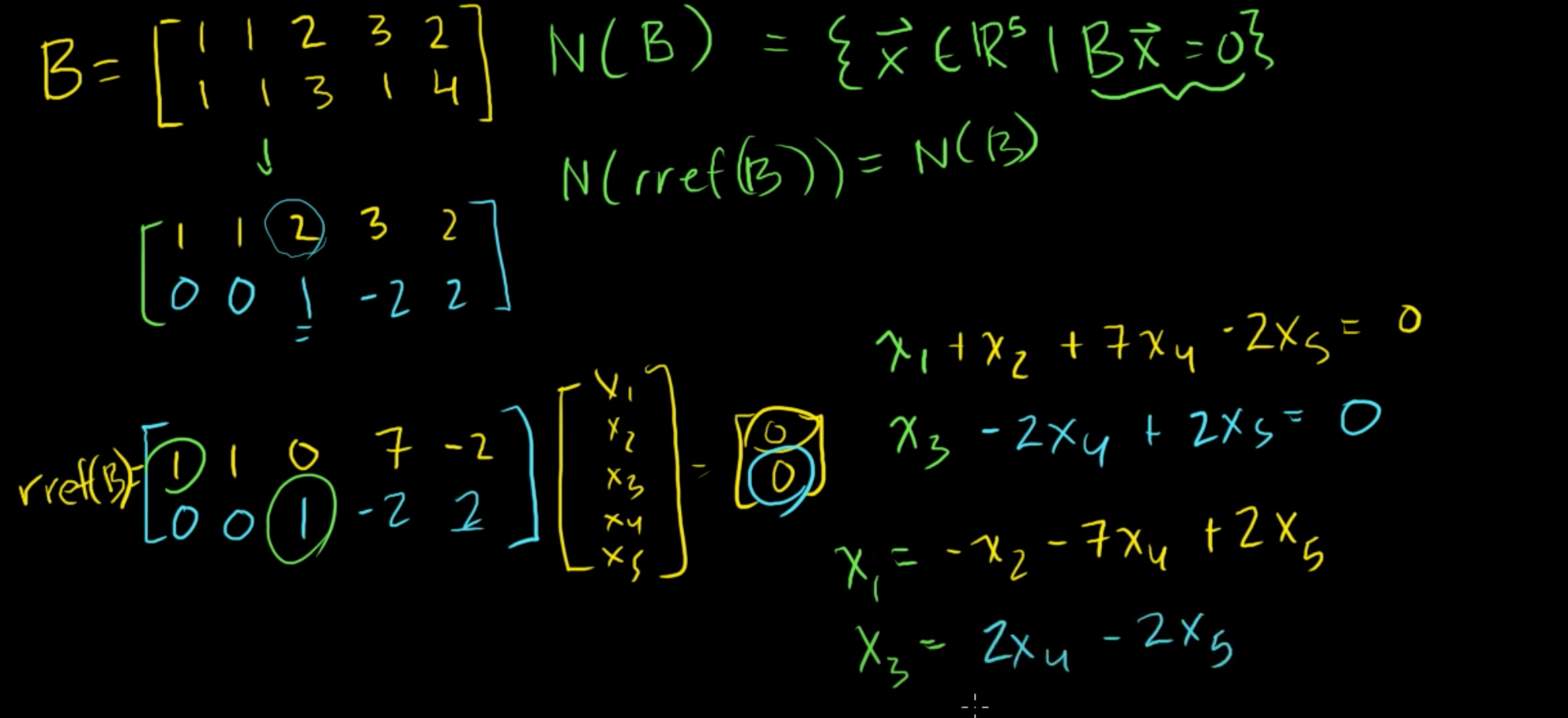
이번 내용은 어려울 게 없다.
그냥 앞의 내용을 다시 정리하고, 이를 기반으로 몇 가지 새로운 사실을 뽑아낸다고 생각하면 된다.
행렬 B [1 1 2 3 2; 1 1 3 1 4;]가 있고, 이 행렬 B의 영공간을 구해보자.
B의 영공간은 Bx = 0을 만족하는 5차원 벡터 x의 집합이고, 기약행사다리꼴행렬의 영공간과 동일하다고 했다.
따라서, 기약행사다리꼴행렬을 구해보면,
[1 1 0 7 -2;
0 0 1 -2 2]가 된다.
여기서 첫째 줄의 x1과 둘째 줄의 x3이 피벗변수이다.
x2 역시 피벗변수가 될 수는 있지만, 식을 2개밖에 못 구하기 때문에 x1을 피벗변수로 설정했다.
피벗 변수에 대한 연립방정식을 세우고, 피벗 변수에 대한 식으로 다시 정리해보자.
x1 = -x2 - 7x4 + 2x5
x3 = 2x4 - 2x5
이다.
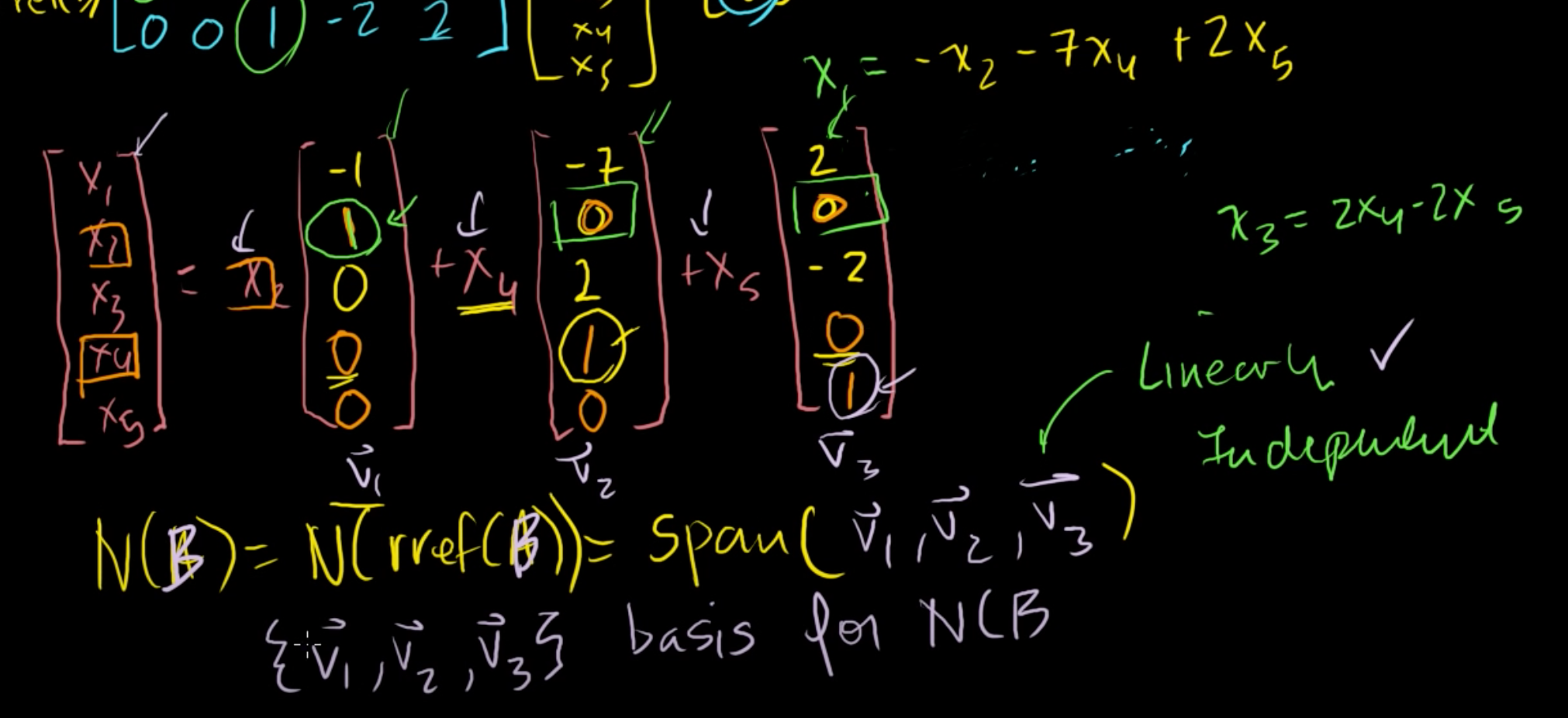
위 식을 다시 써보면, [x1 x2 x3 x4 x5] = x2[-1 1 0 0 0] + x4[-7 0 2 1 0] + x5[2 0 -2 0 1] 이다.
이 때, [-1 1 0 0 0], [-7 0 2 1 0], [2 0 -2 0 1]를 v1, v2, v3라고 하자.
N(B) = N(rref(B)) = span(v1, v2, v3) 가 성립한다.
그런데, v1, v2, v3는 선형독립일까?
이를 알아보기 위해서, 자유변수인 x2, x4, x5를 자세히 보자.
v1의 2번째 스칼라인 1을 만들려면, v2와 v4를 아무리 선형결합 계산해도 구할 수 없다.
왜냐하면 둘 다 0이기 때문에 어떤 x4, x5를 곱하더라도 항상 0이기 때문이다.
v2의 4번째 스칼라 1 역시, v1과 v3에 어떤 x2, x5를 곱하더라도 구할 수 없다.
v3의 5번째 스칼라 1 역시, v1과 v2에 어떤 x2, x4를 곱하더라도 구할 수 없다.
따라서, v1, v2, v3는 선형독립이라는 사실을 알 수 있다.
그리고, v1, v2, v3는 영공간의 basis가 된다.
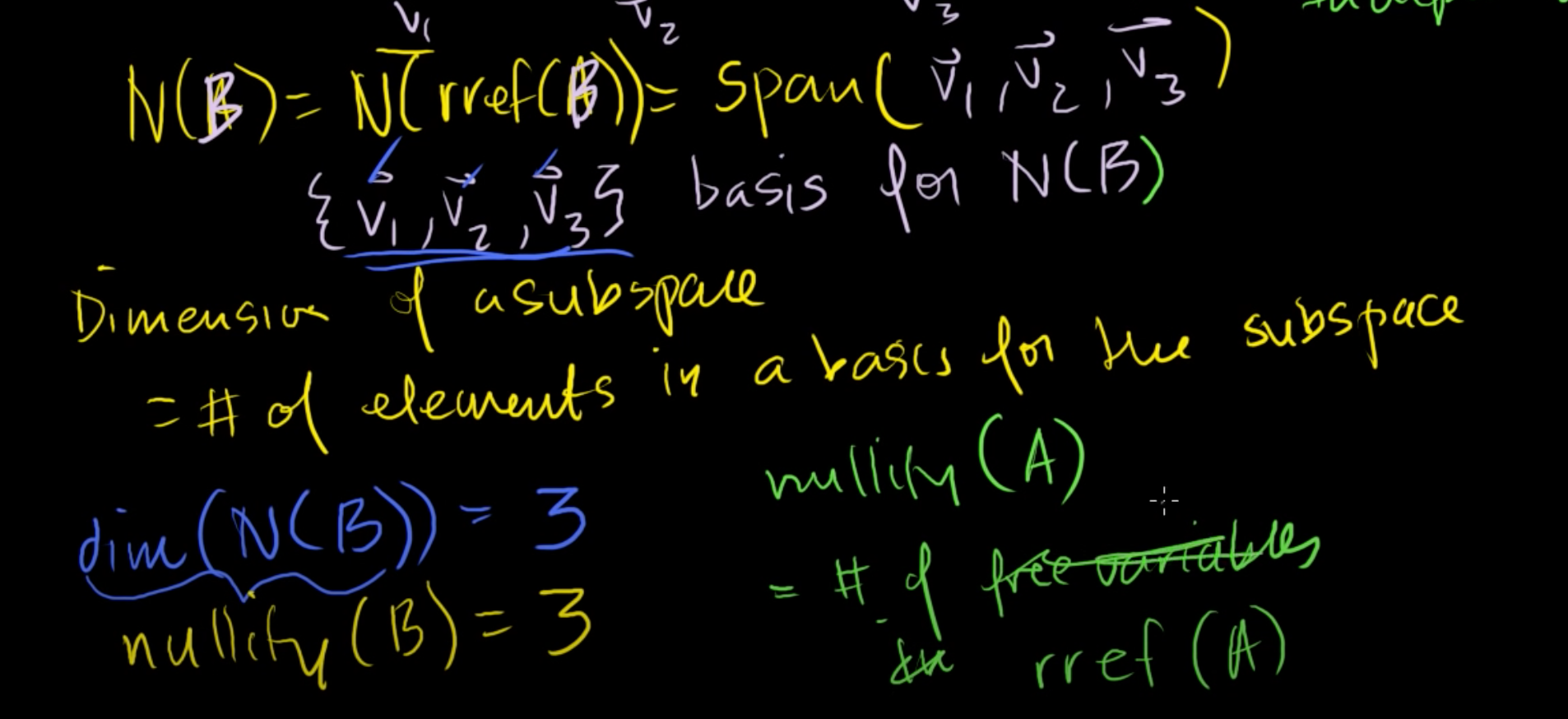
여기까지는 이전에 정리했던 내용의 반복이고, 아래가 새롭게 추가되는 내용이다.
차원이란 부분집합에 대한 기저에 있는 벡터들의 개수를 의미한다.
(부분공간의 기저들은 모두 같은 개수의 요소를 지닌다. 위 경우는 5개)
그래서 B의 영공간의 차원은 3이다.
B의 영공간의 차원은 다른말로 B의 nullity라고도 한다.
B의 nullity 역시 3이 된다.
어떠한 행렬의 nullity는 영공간의 차원으로 구할 수 있고, 영공간의 차원은 자유변수의 개수와 같다.
왜냐하면 자유변수의 개수는 다른 벡터들의 선형결합식으로 나타낼 수 없는 벡터들의 개수이기 때문이다.
그래서 자유변수의 개수는 영공간의 basis 벡터의 개수가 된다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 6-10. 기저 열과 축 열의 관계 (0) | 2023.03.13 |
|---|---|
| 6-9. 열공간의 차원(랭크) (0) | 2023.03.11 |
| 6-7. 열공간의 생성과 방정식 (0) | 2023.03.09 |
| 6-6. 영공간과 열공간의 기저 (0) | 2023.03.08 |
| 6-5. 열공간(Column Space) (0) | 2023.03.07 |