반응형
(1) 그람 슈미트 예제

저번의 예제에서 조금 확장해서, R4 공간에서 벡터 3개로 생성되는 부분공간 V의 정규직교기저를 구해보자.
V = span([0 0 1 1], [0 1 1 0], [1 1 0 0]) 이다.
u1 = v1 / ||v1||
||v1|| = √2
u1 = 1/√2 [0 0 1 1]
u2 = y2 / ||y2||
y2 = v2 - projV1v2 = v2 - (v2 ⋅ u1)u1 = [0 1 1/2 -1/2]
||y2|| = √3/2
u2 = √2/3[0 1 1/2 -1/2]
V = span(v1, v2, v3)
= span(u1, v2, v3)
= span(u1, y2, v3) - u1은 정규화되었고, y2는 직교기저이다.
= span(u1, u2, v3) - 여기까지 구했다.

u3 = y3/ ||y3||
y3 = v3 - projV2v3 = v3 - ((v3⋅ u1)u1 + (v3⋅ u2)u2) = [1 1/3 -1/3 1/3]
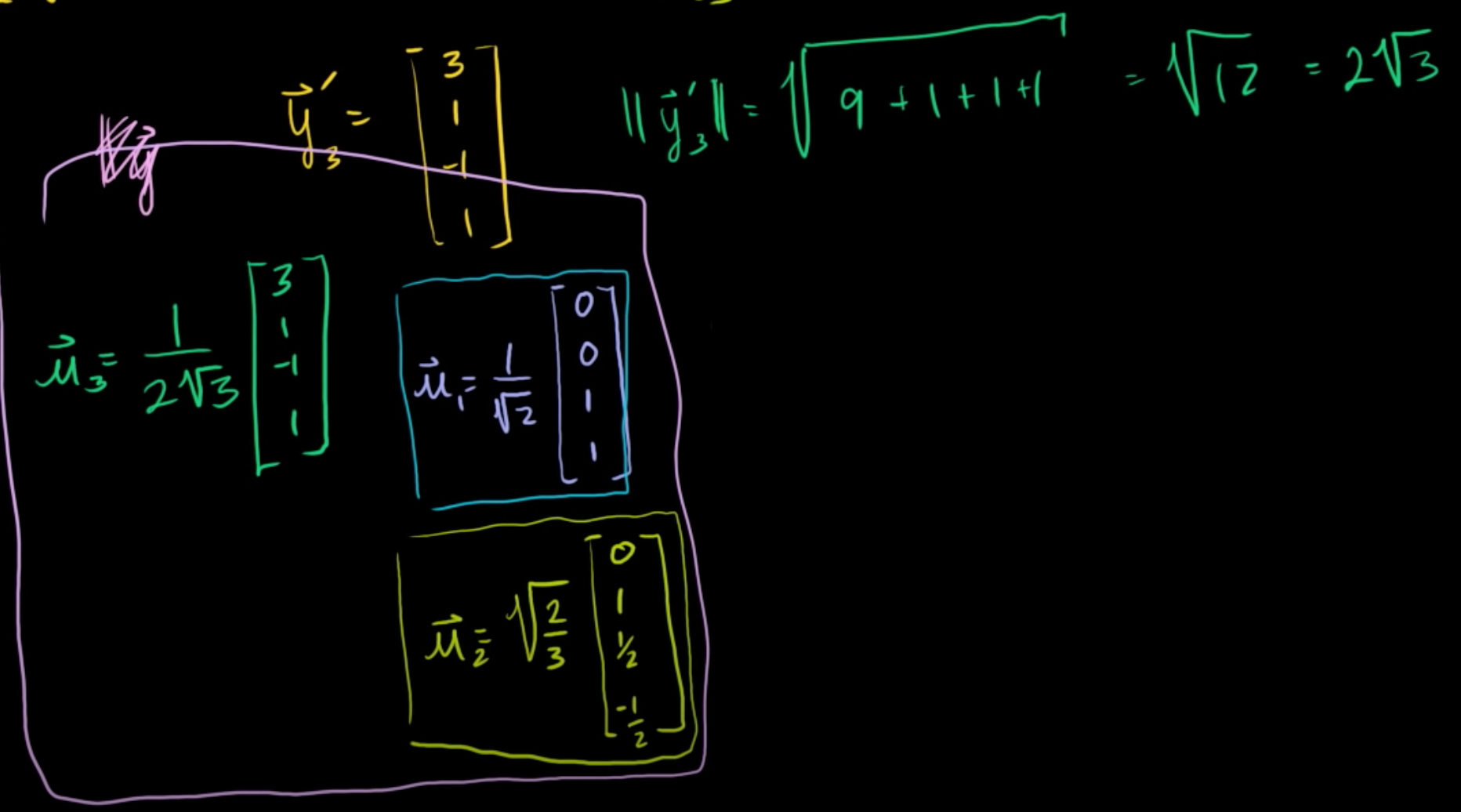
계산이 쉽도록 [1 1/3 -1/3 1/3]을 [3 1 -1 1]로 길게 바꿔주자.
길이가 길어지더라도, 직교하는 것은 동일하기 때문에 상관없다.
||y3|| = √12
u3 = 1/√12 [3 1 -1 1]
V = span([0 0 1 1], [0 1 1 0], [1 1 0 0]) 을
V = span(1/√2 [0 0 1 1], √2/3[0 1 1/2 -1/2], 1/√12 [3 1 -1 1]) 와 같은 정규직교기저로 나타낼 수 있다.
반응형
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 18-2. 고유값 결정식의 증명 (0) | 2023.06.23 |
|---|---|
| 18-1. 고유값, 고유벡터 (0) | 2023.06.22 |
| 17-8. 그람슈미트 예제 1 (0) | 2023.06.15 |
| 17-7. 그람-슈미트 과정 (0) | 2023.06.14 |
| 17-6. 직교기저변환은 각도와 길이를 보존한다 (0) | 2023.06.13 |