(1) 직교기저변환과 길이와 각도 변화

C가 n x n의 정사각행렬이고, 열들이 정규직교집합을 형성한다고 하자.
각 열벡터들은 모두 길이가 1이고, 모두 서로 직교한다.
따라서, 어떤 열을 다른 열과 내적하면 0이 되고, 자기자신과 내적하면 1이 된다.
이러한 행렬을 직교행렬이라고 한다.
직교행렬의 역행렬은 전치행렬과 같다.
앞에서는 이를 기저변환에 주로 활용했다.
x를 표준기저라고 하면, 다른 기저의 좌표로 x를 나타낸 [x]B는 기저변환된 좌표라고 할 수 있다.
x를 [x]B로 변환하려면 C-1을 곱하고, [x]B를 x로 변환하려면 C를 곱하면 된다.
이는 선형변환이고, 직교행렬에서는 어떤 벡터를 변화시키더라도 길이와 각도가 보전된다는 것을 이 글에서 보이고자 한다.
그림으로 표현하면 분홍색 벡터 x가 θ라는 각을 이루고 있으면, C를 곱해서 변환하면 길이는 Cx 각도는 θ가 될 것이다.
길이와 각도가 유지되지 않는다면, 아래의 그림처럼 길어지고 벌어진 벡터가 될 것이다.
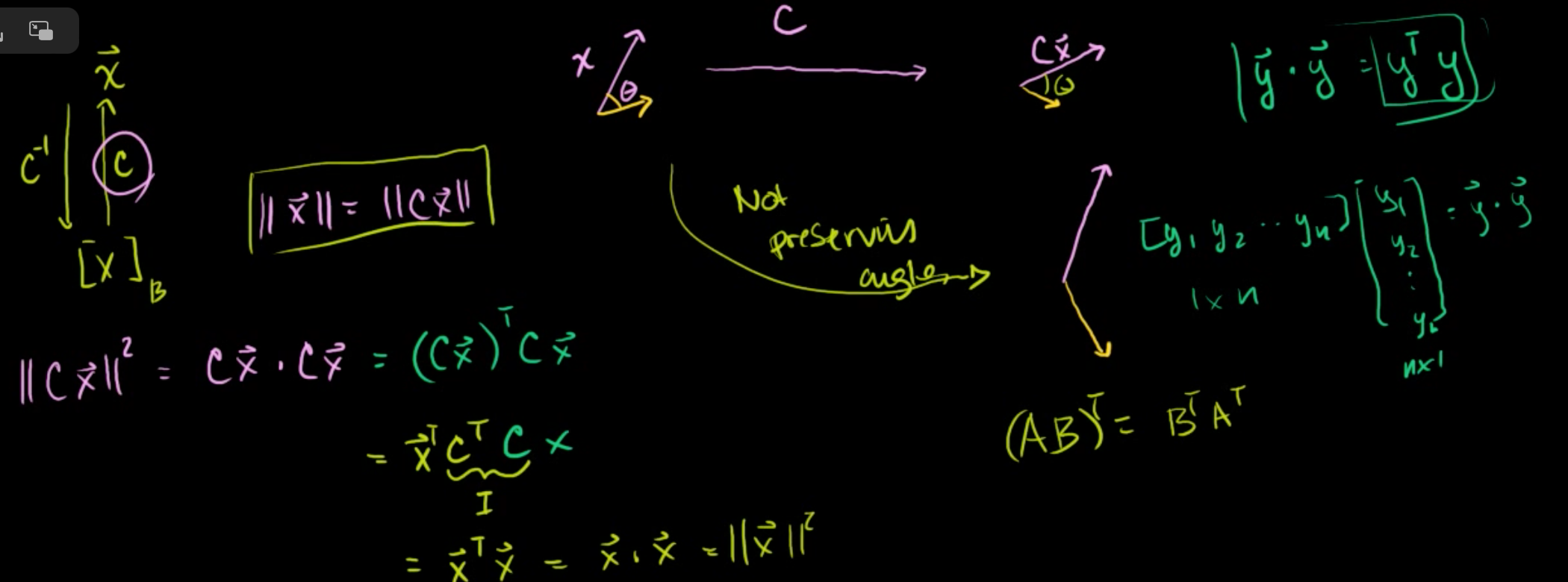
길이가 보전되었는지 알아보자.
길이가 보전되었다면 ||x|| = ||Cx|| 일 것이다.
||Cx||의 길이는 Cx · Cx 로 표현할 수 있다.
자기 자신과의 내적은 y · y = yTy 와 같이 표현할 수 있다.
따라서, ||Cx|| = Cx · Cx = (Cx)TCx = xTCTCx
앞에서 말한 바와 같이 CTC = I 이기 때문에,
xTCTCx = xTx = x · x = ||x||
||Cx|| = ||x|| 가 성립한다.
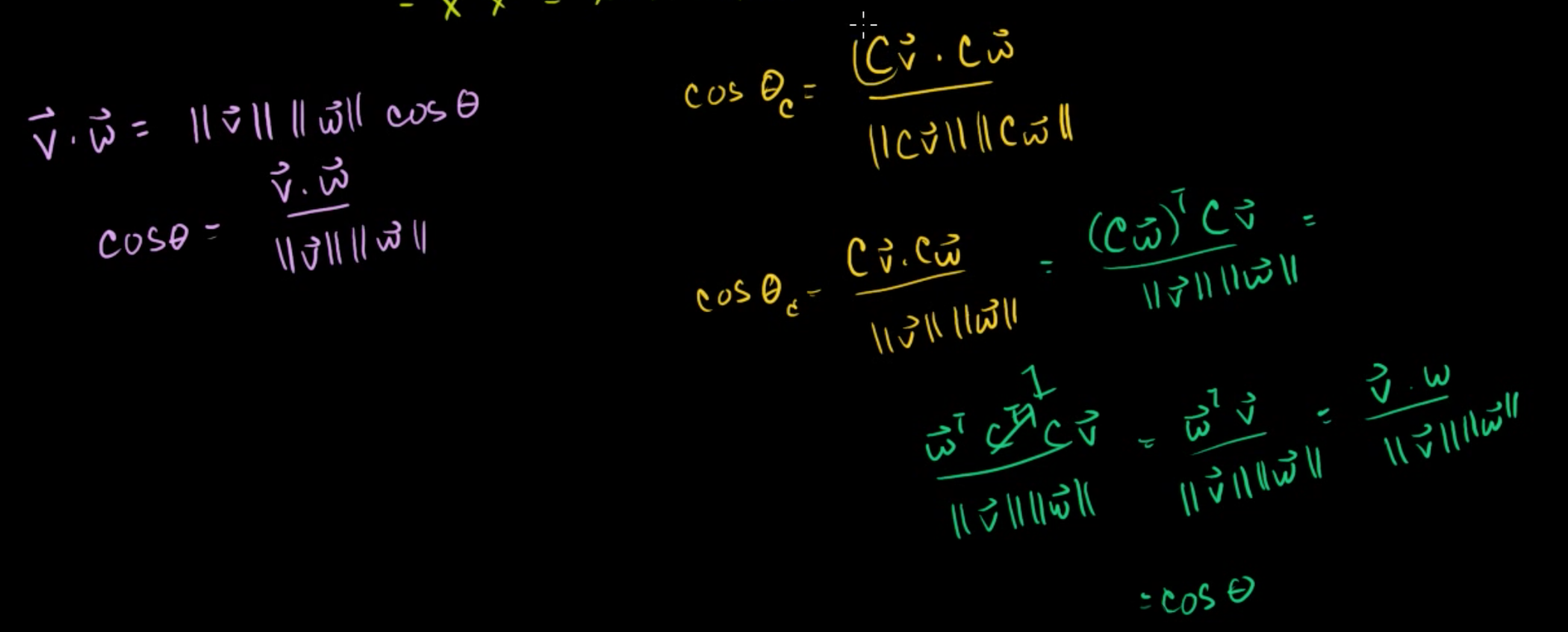
각도 역시 유지되었는지 알아보자.
v · w = ||v|| ||w|| cosθ
cosθ = (v · w) / ( ||v|| ||w|| )
라는 식이 성립함을 앞에서 계속 활용했다.
v와 w에 C를 곱해서 구한 [v]B, [w]B의 각과 v, w의 각이 같은지 계산해보자.
cosθc = (Cv · Cw) / ( ||Cv|| ||Cw|| )
앞에서 길이는 같다고 했기 때문에,
cosθc = (Cv · Cw) / ( ||v|| ||w|| )
내적을 전치행렬의 곱으로 표현하면,
cosθc = ( (Cw)TCv ) / ( ||v|| ||w|| )
= ( wTCTCv ) / ( ||v|| ||w|| )
= ( wTv ) / ( ||v|| ||w|| )
= ( w · v ) / ( ||v|| ||w|| )
= cosθ
따라서, 각도 역시 똑같이 유지된다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 17-8. 그람슈미트 예제 1 (0) | 2023.06.15 |
|---|---|
| 17-7. 그람-슈미트 과정 (0) | 2023.06.14 |
| 17-5. 직교기저 변환행렬을 이용하여 변환행렬 구하기 (0) | 2023.06.12 |
| 17-4. 정규직교기저 활용 예시(정사영 계산) (0) | 2023.06.11 |
| 17-3. 정규직교기저 활용(정사영 계산) (1) | 2023.06.10 |