(1) 행렬식과 평행사변형

행렬 A = [a b; c d]라고 하면, 열벡터 v1 =[a, c], v2 = [b, d]로 표현할 수 있다.
두 열벡터를 좌표 상에 표현하면 우측 그림과 같이 되는데, 만들어지는 평행사변형의 넓이를 구해보자.
증명에 대한 내용은 알고 싶지 않고, 결론만 알고 싶다면 마지막 2줄만 읽으면 된다.
평행사변형의 넓이는 밑변 * 높이로 계산할 수 있고, 수식으로 표현하면
넓이 A = B(밑변) * H(높이) 이다.
이 때, B = ||v1|| 과 같다.
피타고라스 정리에 의해서, H² + ||proj(V2)||² = ||V2||² 이다.
이 때, proj(V2)는 v2가 v1에 투영한 값이다.
proj(x) = {(x·v) / (v·v)} v 이기 때문에, (글 8-5 참조)
proj(V2) = {(V2·V1) / (V1·V1)} V1 으로 계산해줄 수 있다.
이를 대입해서 식을 계속 풀어주자.
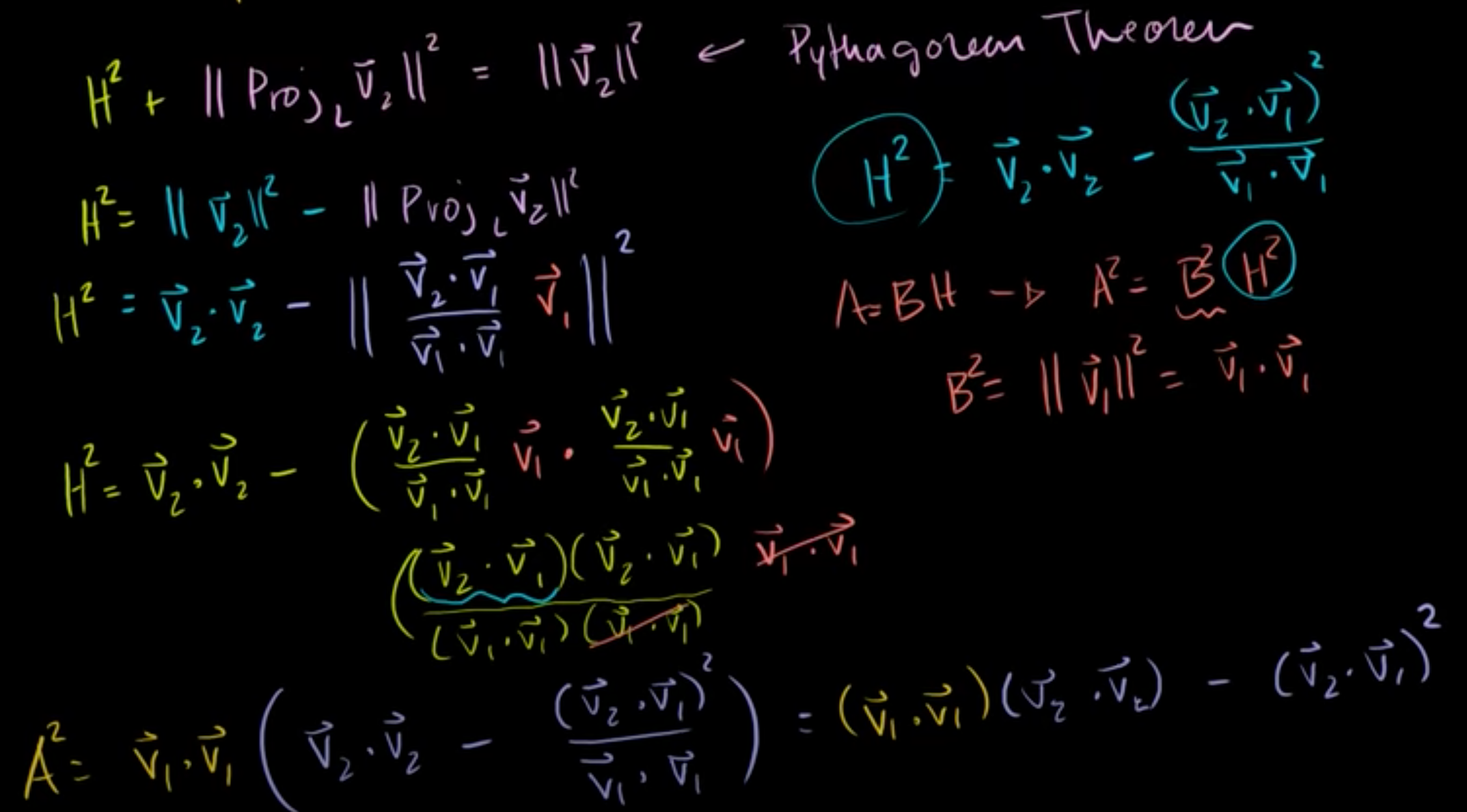
H² = ||V2||² - ||proj(V2)||²
H² = ||V2||² - ||{(V2·V1) / (V1·V1)} V1 ||²
H² = V2·V2 - ||{(V2·V1) / (V1·V1)} V1 ||²
H² = V2·V2 - {(V2·V1) / (V1·V1)}*V1 · {(V2·V1) / (V1·V1)}*V1
H² = V2·V2 - {(V2·V1)(V2·V1) / (V1·V1)(V1·V1)}*(V1 ·V1)
H² = V2·V2 - (V2·V1)(V2·V1) / (V1·V1)
피타고라스의 법칙을 활용하여 H²의 식을 구했으니, 이를 A = BH에 대입해서 넓이를 구해보자.
A² = B²H²
B² = ||V1||² = V1·V1
A² = (V1·V1) * (V2·V2 - (V2·V1)(V2·V1) / (V1·V1))
A² = (V1·V1) * (V2·V2 ) - (V2·V1)²
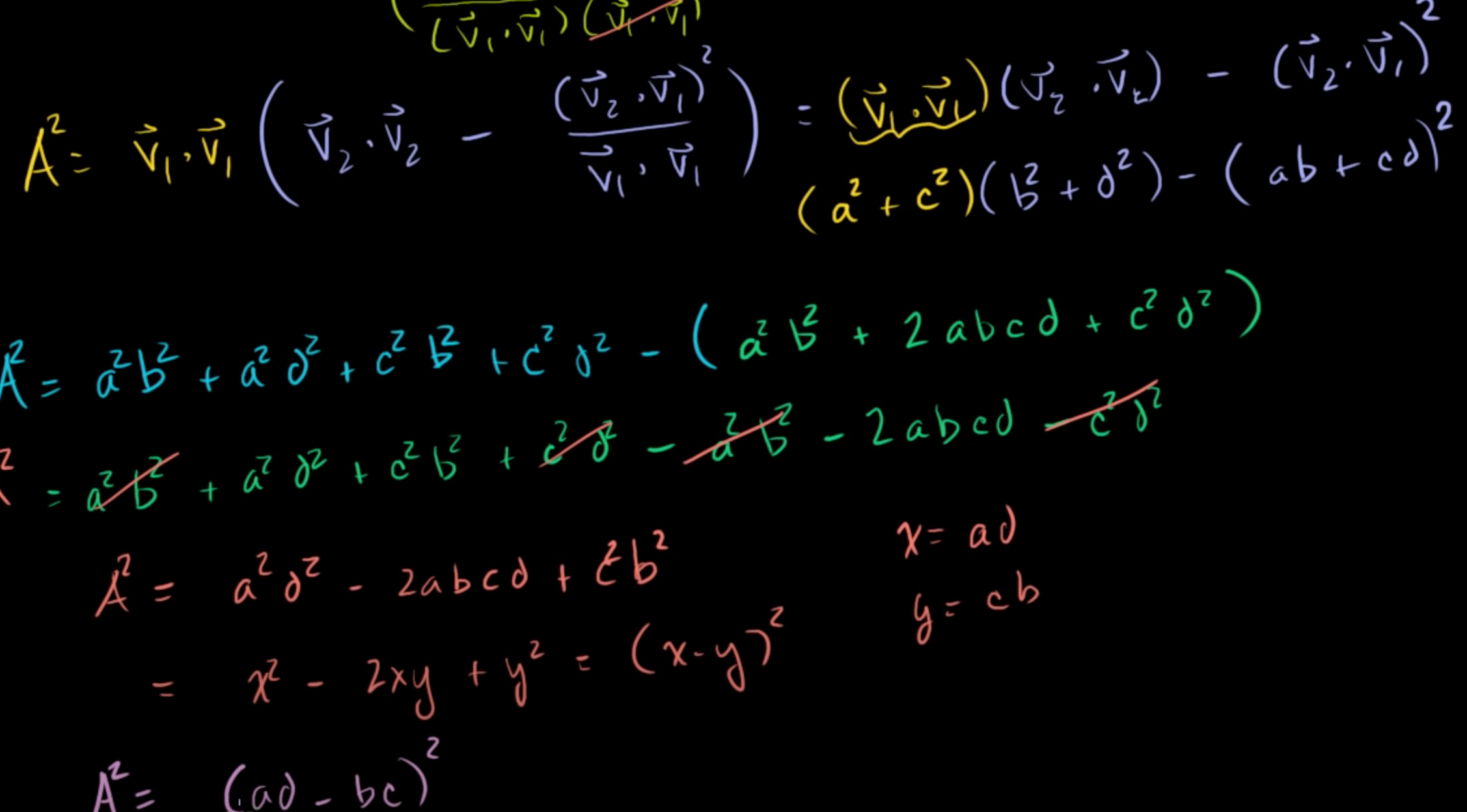
A = [a b; c d] 이고, v1 =[a, c], v2 = [b, d] 이기 때문에
A² = (V1·V1) * (V2·V2 ) - (V2·V1)² 을 실제 값으로 대입해줄 수 있다.
v1·v1 = a² + c²
v2·v2 = b² + d²
v2·v1 = ab+cd
A² = (a²+c²) * (b²+d²) - (ab+cd)²
식을 풀어주면,
A² = a²d² - 2abcd + c²b²
A² = (ad-bc)²
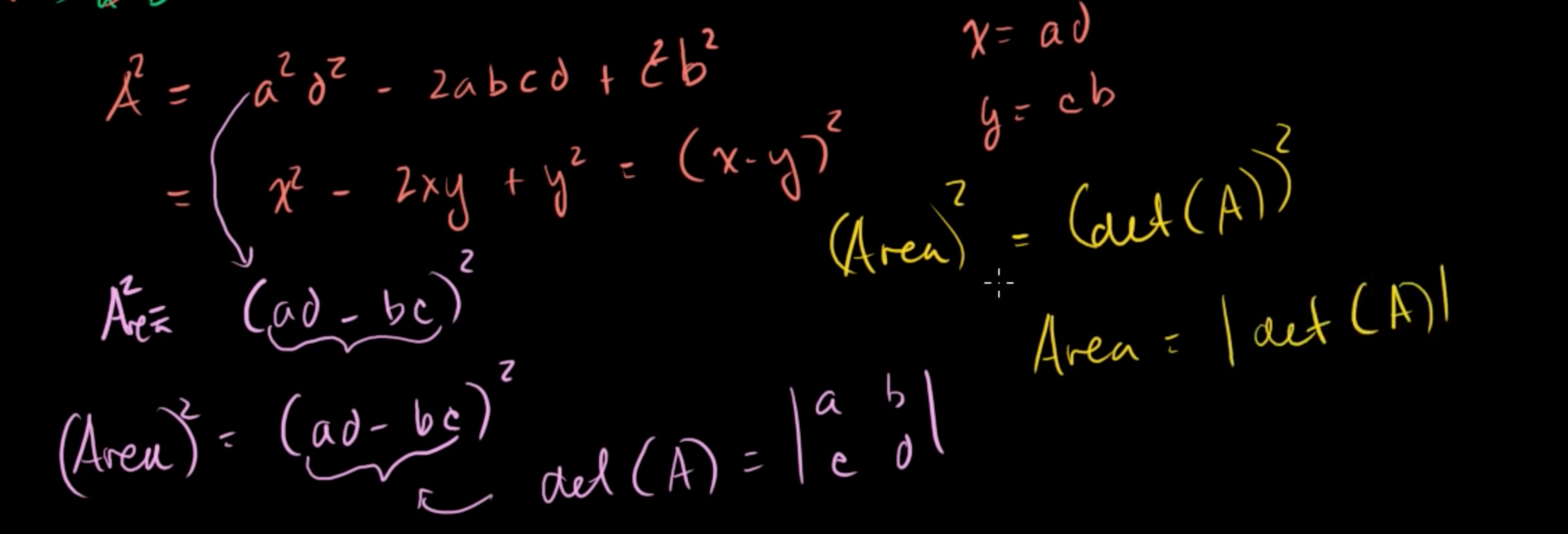
ad-bc = det(A) 와 같기 때문에
A² = (det(A))²
Area = |det(A)|
결론적으로, 행렬식은 열벡터가 만들어내는 평행사변형의 넓이와 같다.
행렬식이 0이라는 것은 두 벡터로 생성되는 평행사변형이 없다는 것이라는 걸 알 수 있다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 13-1. 전치행렬의 열공간, 영공간, 좌영공간 (0) | 2023.04.21 |
|---|---|
| 12-8. 변환에서 행렬식의 의미 (0) | 2023.04.19 |
| 12-6. 행렬식(삼각행렬을 활용한 복합연산) (0) | 2023.04.17 |
| 12-5. 행렬식 (삼각행렬) (0) | 2023.04.16 |
| 12-4. 행렬식(복합 연산) (0) | 2023.04.15 |