(1) 역변환은 선형변환일까?

변환 T가 있고, 가역적인 변환 T는 Rn -> Rn으로 사상한다.
그리고, T의 변환 행렬을 기약행사다리꼴행렬로 나타내면 n x n 단위행렬이 된다고 했다.
그러면, T의 역변환 T-1과 T의 합성함수가 In이고, T와 T-1의 합성함수가 In이다.
이러한 사실들을 알고 있는 상태에서, T-1이 선형변환인지 알아보고자 한다.
선형변환이 되기 위해서는, 덧셈에 닫혀있고 스칼라곱에 대해서 닫혀있다는 사실을 보이면 된다.
T(x+y) = T(x) + T(y)
T(cx) = cT(x)
를 역변환에서도 적용되는지 알아보자.
(2) 역변환이 선형변환이라는 조건 증명.
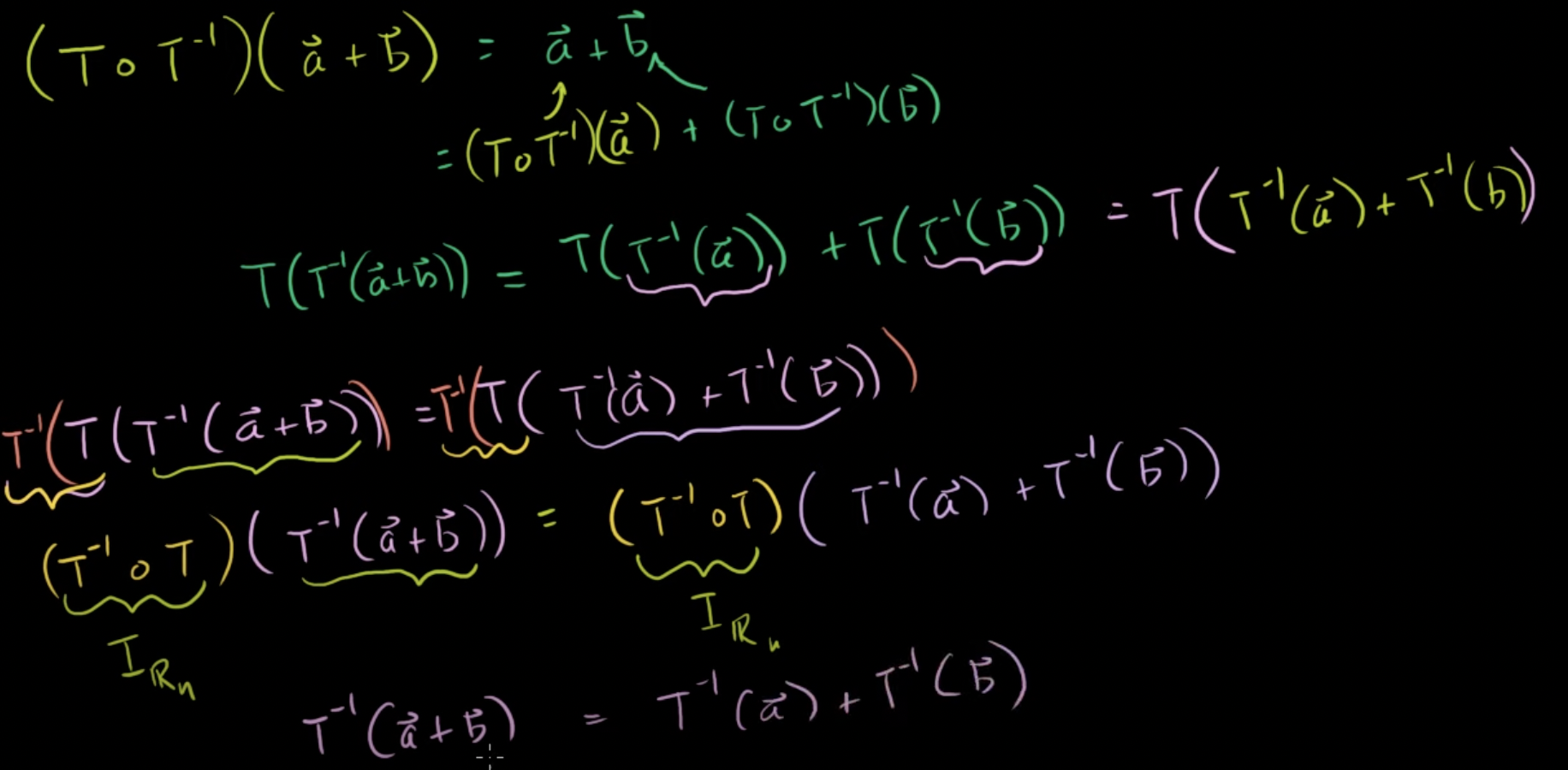
T∘T-1 = In
T∘T-1(a+b) = a+b
T∘T-1(a+b) = T∘T-1(a) + T∘T-1(b)
T(T-1(a+b)) = T(T-1(a) + T(T-1(b)) -> T로 묶어주면
T(T-1(a+b)) = T(T-1(a) + T-1(b)) -> 역행렬을 양변에 곱해준다
T-1(a+b) = T-1(a) + T-1(b)
역변환도 덧셈에 닫혀있다.

T∘T-1 = In
T∘T-1(ca) = ca
T∘T-1(ca) = c(T∘T-1)(a)
T(T-1(ca)) = cT(T-1(a)) -> 역행렬을 양변에 곱해준다
T-1(ca) = cT-1(a)
역변환은 스칼라곱에 닫혀있다.
(3) 결론
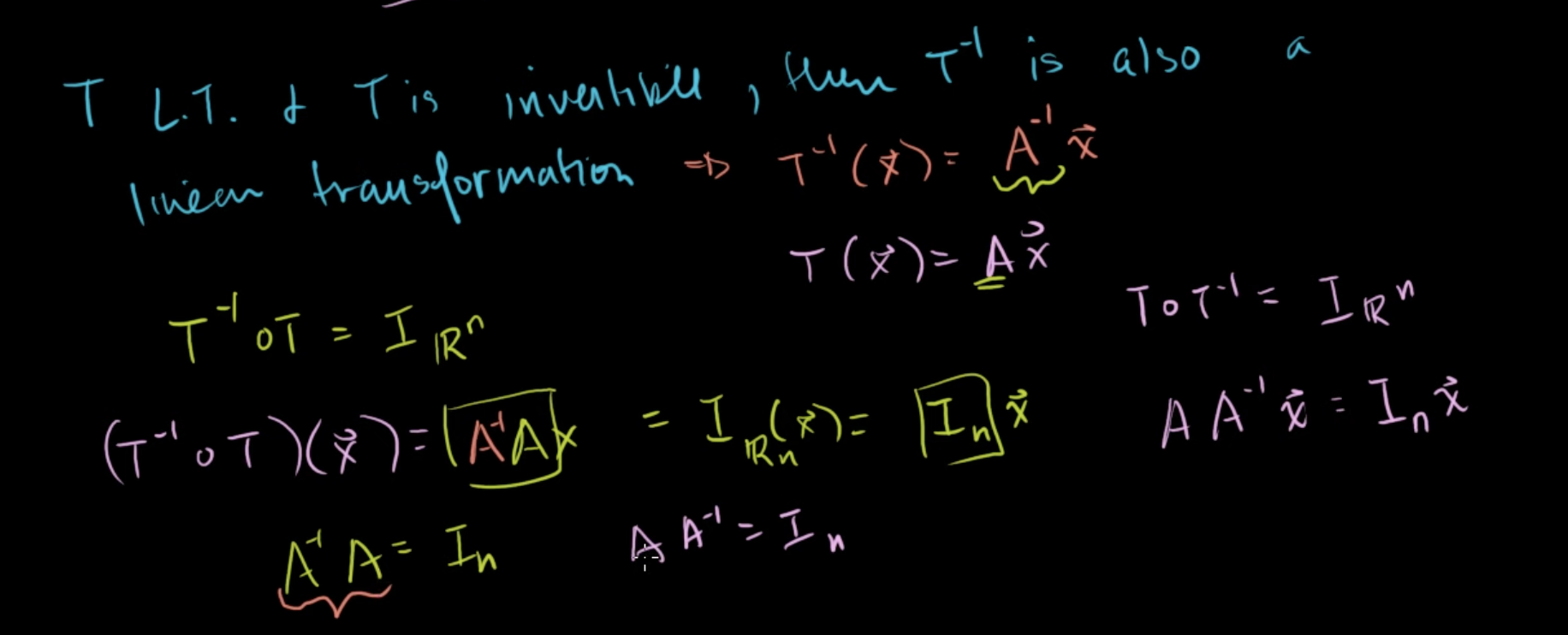
T가 선형독립이고 가역적이라면, T-1 역시 선형변환이다.
T(x) = A(x)
T-1(x) = A-1(x) 이다.
T-1∘T = In
A-1A = In
T∘T-1 = In
AA-1 = In
네 개의 식도 성립한다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 11-2. n x n 행렬의 역행렬 구하기 (0) | 2023.04.11 |
|---|---|
| 11-1. 기약행사다리꼴을 활용한 역행렬 구하기 (0) | 2023.04.10 |
| 10-7. 가역성의 조건(간단한 정리) (0) | 2023.04.09 |
| 10-6. Ax = b가 단사함수가 되는 조건 (0) | 2023.04.07 |
| 10-5. Ax = b에서 가능한 x의 해집합 (0) | 2023.04.06 |