(1) 3차원 공간의 면의 방정식

3차원 공간에서 면의 방정식에 관하여 살펴보자.
임의의 각도에서 모든 방향으로 계속해서 진행되는 면을 그리면,
이 면의 방정식은 ax + by + cz = d 라는 x, y, z로 이뤄진 일차함수가 된다.
면 상의 모든 점 x, y, z는 이 식을 만족한다.
면에 존재하는 점 (x0, y0, z0)가 있다고 정의해 보자.
이 점을 지나가는 면은 무수히 많기 때문에, 이 점 만으로는 면을 정의할 수는 없다.
하지만 점을 정하고, 그 점에서 면으로 직각인 벡터(법선벡터 n)를 명시한다면, 면의 방정식을 구할 수 있다.
법선벡터는 단순히 말하면 면의 모든 벡터에 직각을 이루는 벡터이다.
면 위의 노란색 벡터(a)가 있다고 가정하고, 법선벡터(n)가 있다면,
우리는 벡터 각도의 정의에 따라서 두 벡터의 내적, n∙a가 0일 경우에 한해서만 두 개의 벡터가 직각을 이룬다.
이 사실은 면 상에 존재하는 모든 벡터에 관하여 유효하다.
그렇다면 n+ (x0, y0, z0) 라는 식을 선형 방정식 ax+by+cz=d 의 기본 형태로 바꿔 쓸 수 있을까?
면 상에 존재하는 파란색 점(x0, y0, z0)을 위치벡터로 표현하면, 위치벡터 x0를 다음과 같다고 할 수 있다.
파란색 x0를 스칼라 [x0;y0;z0]로 정의할 수 있다.
이 벡터가 완전히 면에 속하는 것은 아니고, 원점에서 시작해 화살표의 끝이 면 위에 존재하는 벡터이다.
벡터 자체는 면 위에 그려진 것이 아니다. 그저 면의 한 점을 가르키고 있을 뿐이다.
비슷하게 다른 벡터 x(노란색)를 [x;y;z]라고 정의해보자.
벡터 x 역시 면 상에 존재하지 않으며, 원점으로부터 시작하며, 면 상의 한 점을 나타내는 위치벡터이다.
x0와 x는 둘 다 원점에서 시작하며, 면 상의 한 점을 가르키는 위치벡터이다.
왼쪽의 면을 평평하게 그려보면, 우측의 그림과 같이 된다.
x0와 x 이 벡터들이 면 상에 존재하지 않지만, 이 벡터들을 이용해서 면에 존재하는 벡터를 구할 수 있다.
벡터 x에서 벡터 x0를 빼는 것이다.
x-x0을 초록선으로 표현하면, 면 위에 존재하는 벡터가 나온다.
그러므로 x-x0은 법선벡터 n과 직각을 이룰 것이다.
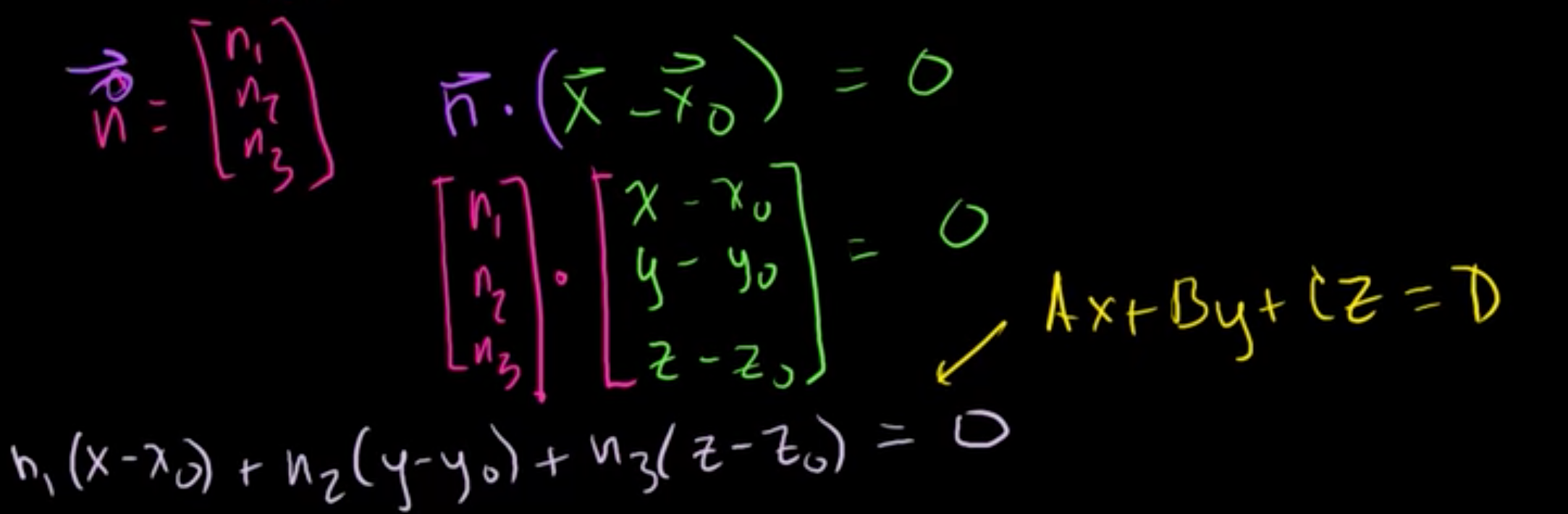
아까 법선벡터와 직각을 이룬다고 했으며, 법선벡터 n [n1, n2, n3]이라고 부르도록 하자.
법선벡터 n은 (x-x0)와 직각을 이루기 때문에, n와 (x-x0)의 내적 값은 0이 될 것이다.
위 그림의 식을 풀어보면, n1(x-x0)+n2(y-y0)+n3(z-z0)=0 라는 식이 나오게 된다.
이를 약간 다시 정리해보면, ax+by+cz=d 의 형태로 선형 방정식을 표현할 수 있다.

위의 식이 맞는지, 예를 들어서 살펴보자.
어떠한 면이 있으며, 면의 법선벡터가 [1, 3, -2] 이며, 이 벡터가 면 상의 한 점을 지난다고 가정하자.
법선벡터와 점은 꼭 직교해야만 하는 것은 아니다.
면 상의 한 점을 [1, 2, 3]이라고 하고, 이 면에 대한 식을 구해야한다고 해보자.
면의 다른 임의의 점 [x, y, z]를 벡터 x가 가르키며, 벡터 x와 벡터 xc의 차이를 나타내는 벡터를 구한다면, 그 벡터는 면 상에 존재한다.
왜냐하면, 두 점이 둘 다 면 상에 존재하므로 두 개의 벡터의 차이는 면 위에 존재하기 때문이다.
두 점의 차이를 구해보면, x-x0=[x-1; y-2; z-3] 이고, 이 것은 면 위에 존재한다.
그리고 법선벡터와 수직할 것이다.
그러므로, 법선벡터 [1; 3; -2]와 이 벡터 [x-1; y-2; z-3]을 내적시키면 0이 나와야한다.
왜냐하면 법선벡터는 면 상의 모든 것과 수직하기 때문이다.
이 식을 풀면 (x-1)+3(y-2)-2(z-3)=0이 되며,
이 식을 정리하면 x+3y-2z=1 이 된다.
이처럼, 면 위에 존재하는 두 점과 법선벡터를 활용하면, 두 점의 차이가 법선벡터와 직각을 이루어야 한다는 점을 활용하여 면의 방정식을 구할 수 있다.
하지만, 위의 연보라색 공식을 사용하면 더 쉽게 구할 수 있다.
1(x-1)+3(y-2)+-2(z-3)=0 이라는 단순한 식을 풀면, 동일한 면의 방정식을 구할 수 있다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 4-7. 벡터의 외적과 Sin값 (0) | 2023.02.17 |
|---|---|
| 4-6. 벡터의 외적 (0) | 2023.02.15 |
| 4-4. 벡터 사이의 각도, 수직과 직교의 차이 (0) | 2023.02.08 |
| 4-3. 벡터의 삼각부등식 (0) | 2023.02.02 |
| 4-2. 코시슈바르츠 부등식의 증명 (0) | 2023.01.29 |