1. 벡터의 합, 스칼라 곱

앞에서 정리하기도 했고, 간단한 내용이지만 다시 한번 짚고 넘어가자.
a1, a2부터 an까지의 값을 가지는 벡터와 b1, b2부터 bn까지의 값을 가지는 벡터를 더한다면, 단순히 두 벡터들의 대응되는 성분들을
서로 더하면 된다.
즉, a1 + b1, a2 + b2, ..., an + bn이 된다.
어떤 실수 c를 어떤 벡터 a1, a2, ... , an에 곱한다면 벡터의 각 성분에 스칼라를 곱하면 된다.
즉, ca1, ca2, ... , can이 된다.
이 곱셈은 단순히 벡터의 크기만 키운거일 뿐, 벡터의 곱이라고 하기는 힘들다.
2. 벡터의 내적(Dot Product)

벡터의 내적은 a·b로 표현하며, 십자 형태의 기호는 사용하지 않는다.
그 기호는 벡터의 외적에 사용되기 때문이다.
내적은 외적과는 다르게 수학적으로 상당히 간단하다.
예를 들어 벡터 a1, a2, ... , an이 있고, 벡터 b는 b1, b2, ... , bn가 있다고 해보자.
두 벡터의 내적은 대응하는 성분끼리의 곱과 같다.
그러므로 a1 × b1 + a2 × b2 + ... + an × bn 이 되며, 이 값은 벡터가 아닌 단순 실수인 스칼라 값을 가지게 된다.
이와 같은 몇 가지 예시를 들어 보면, 벡터 (2, 5)와 벡터 (7, 1)을 내적한다면 그 결과는 2 × 7 + 5 × 1 = 19가 된다.
그러므로 이 두 벡터의 내적값은 19이다.
벡터 (1, 2, 3)과 벡터 (-2, 0 ,5)와 내적하면, 1 × (-2) + 2 × 0 + 3 × 5 = 13이다.
3. 벡터의 길이(Length)

벡터의 길이는 우리가 아는 일반적인 길이의 정의와 일관적이다. 것입니다
벡터 a에 대한 길이를 표현한다면, 두 줄을 벡터의 좌우에 두면 된다.
벡터 a의 길이(||a||)는 각각의 성분을 제곱하고 모두 더한 값의 제곱근과 같다.
a1² + a2² + ... + an² 까지 더하고, 루트를 씌워주면 된다.
꽤 간단하다.
만일 이 벡터 b가4 (2,5)라고 한다면, 벡터 b의 크기는 √2²+5² 인 √29이다.
그래프 상으로 그려보면, 피타고라스 정리의 형태라는 것을 알 수 있다.
이 같은 정의는 50개의 성분을 가진 50차원 벡터의 길이에서도 동일하게 적용된다.
시각화할 수 없는 벡터의 길이를 추상화하여 표현할 수 있다.
길이와 내적은 연관성이 있다.
만일 벡터 a가 자기 자신과 내적을 한다면, a1² + a2² + ... + an²이다.
그리고 벡터 a의 길이는 √ a1² + a2² + ... + an²이다.
즉, 벡터의 길이에 대한 정의를 내적을 이용하면, 길이는 스스로 내적한 값의 제곱근이라고 표현할 수 있다.
또한 양쪽을 제곱하면, 길이의 제곱은 벡터 a와 그 자신을 내적한 것과 같다고도 할 수 있다.
4. 벡터 내적의 교환법칙, 분배법칙, 결합법칙

첫번째로, 내적에 교환법칙이 성립하는지 알아보자.
V·W = W·V인가?
벡터 V를 v1, v2, ... , vn이라고 가정하고, 벡터 W를 w1, w2, ... ,wn이라고 가정하자.
V·W는 v1 × w1 + v2 × w2 + ... + vn × wn 이고,
W·V는 w1 × v1 + w2 × v2 +... + wn × vn 이다.
v1, w1은 실수(스칼라)이기 때문에 v1 x w1= w1 × v1 이다.
즉, 내적에서는 교환법칙이 성립되기 때문에 곱의 순서가 중요하지 않다.
두번째로, 내적에 분배법칙을 적용할 수 있을까?
x1, x2, ... , xn인 벡터 x가 있고, 이를 v + w에 x를 곱해보자.
만약 분배법칙이 성립한다면, (v + w)·x는 v·x + w·x와 같아야 한다.
v + w는 v1 + w1, v2 + w2, ..., vn + wn이다.
그 다음 x1, x2, ..., xn을 내적한다면, (v1 + w1) × x1 + (v2 + w2) × x2 + ... + (vn + wn) × xn이 될 것이다.
즉, (v + w) · x = (v1 + w1) × x1 + (v2 + w2) × x2 + ... + (vn + wn) × xn 이다.
v·x + w·x는 (v1x1 + w1x1) + (v2x2 + w2x2) + ... + (vnxn + wnxn) 이다.
여기서 x로 묶으면 (v1+w1)x1 + (v2+w2)x2 + ... + (vn+wn)xn이 된다.
두 식은 같은 결과를 나타낸다.
따라서 이 식은 분배한 식과 같고, 내적에서도 분배법칙이 성립한다.
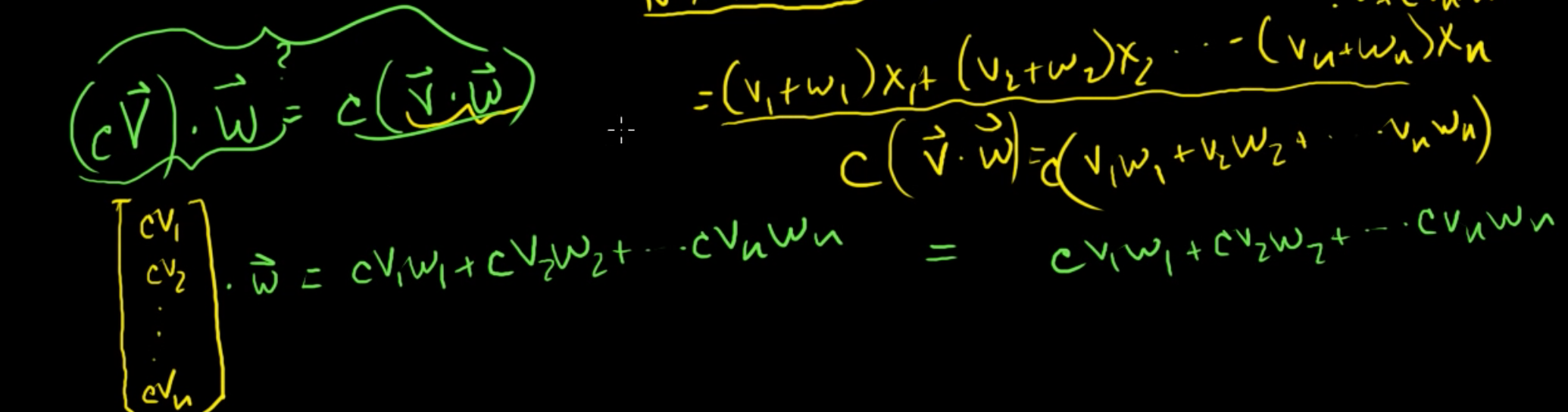
세번째로, 내적에 결합법칙을 적용할 수 있을까?
스칼라 c와 어떤 벡터 v에 곱하고 w를 내적한 값이, 벡터 v와 w를 내적한 값에 스칼라 c를 곱한 값이 같다면 결합법칙이 성립한다.
c × v = c × v1, c × v2... c × vn 이고,
이를 w와 내적하면 cv1w1 + cv2w2 + ... + cvnwn이 된다.
v·w는 v1w1 + v2w2 + ... + vnwn 이고,
이를 c와 곱하면 cv1w1 + cv2w2 + ... cvnwn 이다.
두 식의 값이 같기 때문에 이들은 결합법칙이 성립한다.
결론적으로, 일반적인 수에 대한 분배법칙, 결합법칙, 교환법칙이 벡터와 내적에 대해서도 동일하게 적용할 수 있다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 4-3. 벡터의 삼각부등식 (0) | 2023.02.02 |
|---|---|
| 4-2. 코시슈바르츠 부등식의 증명 (0) | 2023.01.29 |
| 3-2. 부분공간의 기저 (0) | 2023.01.27 |
| 3-1. 선형부분공간 (1) | 2023.01.26 |
| 2-3. 선형독립, 선형종속 추가 (수식 정의, 증명) (1) | 2022.11.30 |