1. 단위벡터(Unit Vectors)

벡터 v가 2-튜플 (2, 3)이라고 한다면, 이를 어떻게 단위벡터를 활용하여 표현할 수 있을까요?
그러기 위해 일단은 단위벡터를 정의해본다면, 단위 벡터는 길이가 '1'인 벡터이다.
단위 벡터는 종종 알파벳 위에 곡절부호(circumflex)를 쓰고, '햇'이라고 읽는다. v^로 표기되며, '브이 햇'(v hat)으로 읽는다.
단위벡터 i는 수평방향으로 1단위만큼만 움직이는 벡터라고 하고,
단위벡터 j는 수직방향으로 1단위만큼만 움직이는 벡터라고 정의한다면
어떤 2차원 벡터든지 간에 i와 j의 합으로 표현할 수 있다.
벡터 v는 (2, 3)이기 때문에, 2i^ + 3j^으로 표현될 수 있다.
(-1, 4)인 벡터 b는 -1i^ + 4j^으로 표현될 수 있다.
벡터 v + 벡터 b를 연산하기 위해서는, 단위벡터끼리 연산을 하면 된다.
따라서, 벡터v + 벡터b는 i^ + 7j^으로 표현될 수 있다.
이처럼 벡터는 단위벡터 표기법을 사용해서 나타낼 수도 있으며, 열벡터를 사용하여 표현할 수도 있다.
*** 단위벡터의 연산.
단위벡터는 크기가 1인 벡터, 즉 길이가 1이어야한다.
따라서, (3,4)인 벡터의 크기는 5이기 때문에 이 벡터의 단위벡터는 (3/5, 4/5)이다.
아래의 퀴즈의 값은 5가 된다.

2. 직선의 매개변수 표현
n차원에서 직선의 방정식을 어떻게 벡터를 활용하여 표현하는지 알아보도록 하자.

벡터 V가 (2,1)이고, S라는 집합이 실수 스칼라 c와 벡터 V의 곱으로 이뤄진 집합이라면 위와 같이 좌표에 그려질 수 있다.
즉, 집합 S는 동일선상에 존재하는 벡터의 집합이다.
왜냐하면, c * V인 벡터를 위치벡터로 본다면, S는 원점을 지나며 1/2의 기울기를 갖는 직선상에 존재하는 위치벡터로 표현할 수 있기 때문이다.
그렇다면, 1/2의 기울기를 가지면서 원점을 지나지 않는 직선을 그리려면 어떻게 표현할 수 있을까?
아래처럼 하면 된다.

벡터 X가 (2,4)라고 해보자.
벡터 V에 벡터 X를 더해주면, 파란색 직선 상에 있는 한 점을 나타내게 된다.
하늘색 직선을 표현하는 집합 L을 벡터를 활용해 표현하면 (벡터X + 실수t * 벡터V)라고 할 수 있다.
위치벡터의 관점에서 이 벡터의 종점은 2차원 평면 위에 존재하는 하늘색 직선 상의 어느 점이다.
기존 대수학에서는 직선을 정의하기 위해 y=mx + a와 같은 식으로 표현했기 때문에,
이러한 방식은 직선을 정의하는데 상당히 어리석은 방법이라고 생각할 수도 있다.
하지만, 이상한 집합을 정의하고 집합과 벡터에 대해서 생각하게 만들며 벡터를 더하는 이유가 있다.
왜냐하면 2차원을 넘어선 모든 차원에서 이러한 방식이 더욱 쉽게 표현하는 방식이기 때문이다.
10차원, 20차원 모두 이런 식으로 표현하면 직선을 간단하게 표현할 수 있다.
실제로 어떻게 표현하는지 아래의 그림을 통해 알아보자.

벡터 a가 (2,1), 벡터 b가 (0,3)이라고 할때, 초록색 직선을 구하려면 어떻게 해야할까?
기울기를 구하는 방법은 벡터b-벡터a를 하면 된다.
(벡터 a - 벡터 b를 하더라도 결과는 같다. 왜냐하면 t는 모든 실수이기 때문에, -1을 곱해주면 -1(a-b)의 값은 b-a이다.)
이를 집합 L로 표현하면, 실수 t * (b-a) + a 또는 실수 t * (b-a) + b로 표현할 수 있다.
흥미롭게도, 벡터 b를 더해주나 벡터 a를 더해주나 결과로 나오는 직선은 동일하다.
벡터 a와 b를 L에 대입해서 풀어보면, 초록색 식이 나오는데, x에 대한 식과 y에 대한 식으로 풀어보면
x = 2t , y = 2t+3이 된다. (y에 대해 정리하면, y = x + 3이 된다.)
즉, 우리가 일반적으로 대수학에서 보는 것과 같은 직선의 방정식을 구할 수 있다.
3차원으로 확장해보면 아래와 같다.
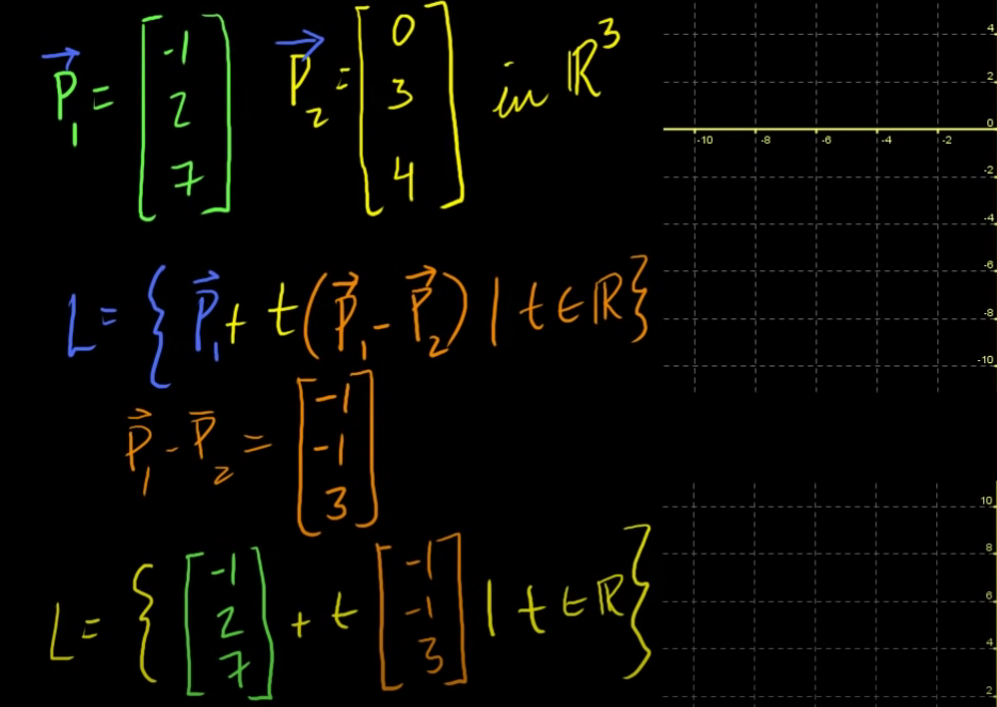
3차원 좌표에 존재하는 p1과 p2를 정의하고, 이 두 벡터를 지나는 직선을 구하려면 L과 같이 식을 세우면 된다.
(p1-p2말고 p2-p1해도 되며, 더해주는 값이 p1이 아니라 p2이어도 상관없다.)
이 식에 p1과 p2를 대입해보면
x = -1 -1t
y = 2 -1t
z = 7 + 3t
와 같은 세개의 매개변수 방정식이 나온다.
3차원에서는 직선을 정의하는 유일한 방법은 위와 같은 매개변수 방정식밖에 없다.
일반적으로 우리가 대수학에서 배웠던 x + y + z = k 와 같은 방정식은 직선이 아니라 평면에 대한 식이다.
3차원 이상의 공간에서 직선이나 곡선, 아니면 비행경로와 같은 것을 표현하려면 매개변수 방정식을 사용해야만 한다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 2-3. 선형독립, 선형종속 추가 (수식 정의, 증명) (1) | 2022.11.30 |
|---|---|
| 2-2. 선형독립, 선형종속 (0) | 2022.11.29 |
| 2-1. 선형결합과 생성 (0) | 2022.11.28 |
| 1-2. 벡터 (벡터의 덧셈과 곱셈) (0) | 2022.11.24 |
| 1-1. 벡터 (벡터와 실좌표공간) (0) | 2022.11.23 |