(1) V와 V의 직교여공간으로 Rn 표현하기

Rn의 부분집합은 부분공간 V가 있고, V의 직교여공간인 V⊥가 있고 이것 또한 Rn의 부분집합이다.
앞에서 정리한 것처럼 dim(V) + dim(V⊥) = n이다.
두 부분공간이 공통으로 가지는 벡터가 존재할까?
x라는 벡터가 V와 V⊥의 원소라고 가정해보자.
둘이 직교하기 때문에 V에 속하는 모든 v에 대해서 x·v = 0 이고,
x·x = 0 역시 성립한다.
자기 자신과의 내적은 길이의 제곱과 같기 때문에, ||x||²=0 이라는 의미이고, 이는 x = 0 일때만 성립한다.
따라서, V와 V⊥의 교집합 원소는 0이고, 이를 그림으로 그려보면 위와 같이 된다.
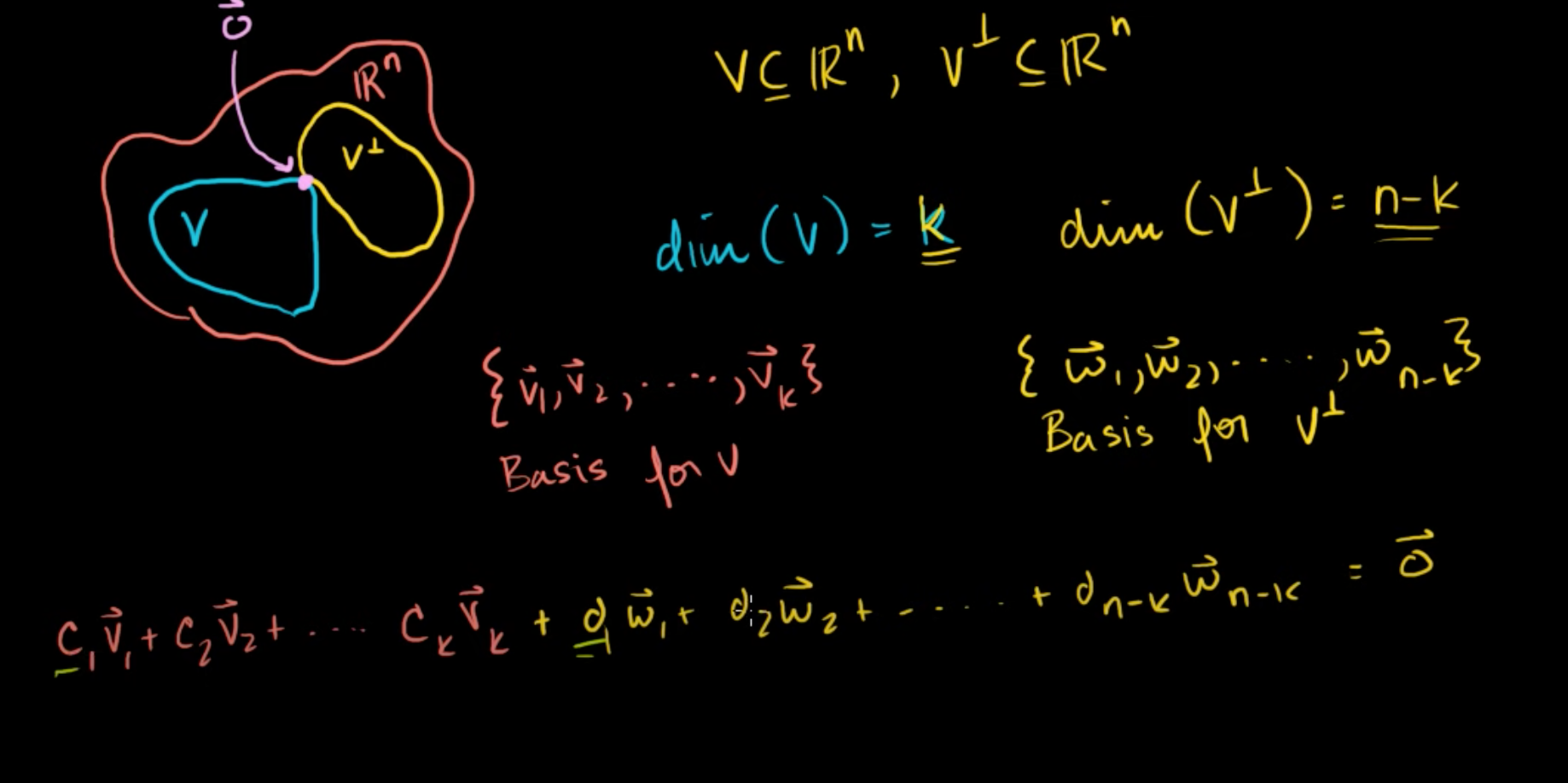
dim(V) = k 라고 하면, dim(V⊥) = n-k 가 된다.
차원은 기저에 필요한 선형독립한 벡터의 개수를 말한다.
기저를 표현해보면,
V의 기저는 {v1, v2, ..., vk}
V⊥의 기저는 {w1, w2, ..., wn-k} 이다.
V와 V⊥의 임의의 벡터는 기저벡터들의 선형결합으로 표현될 수 있다.
이 두 개의 집합을 합치면 Rn 전체의 벡터와 기저를 얻을 수 있는지 알아보자.
Rn의 원소는 (c1v1+c2v2+ ... + ckvk) + (d1w1+d2w2+ ... + d(n-k)w(n-k)) 으로 표현할 수 있고,
0이라고 해보자.
만약, c1, c2, ..., ck, d1, d2, ..., d(n-k)가 모두 0일 때만 위의 식이 성립한다면, v1, v2, ..., vk, w1, w2, ..., w(n-k)가 모두 선형독립하다는 것을 알 수 있다.
그리고 서로에 대해 모두 선형독립하다면, 이들이 Rn의 기저가 될 수 있다.
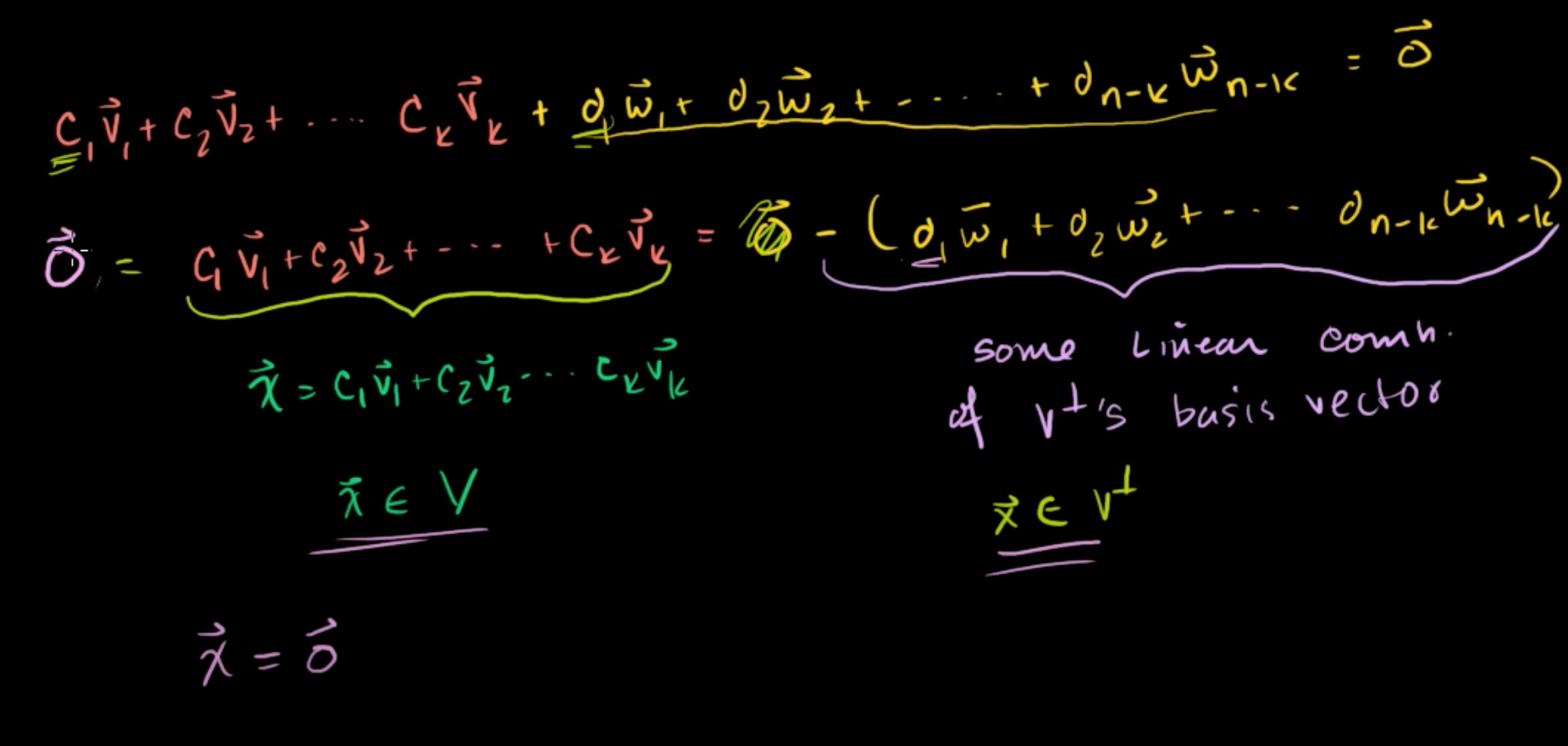
(c1v1+c2v2+ ... + ckvk) + (d1w1+d2w2+ ... + d(n-k)w(n-k)) = 0 에서
(d1w1+d2w2+ ... + d(n-k)w(n-k))를 우항으로 넘겨주면,
(c1v1+c2v2+ ... + ckvk) = -(d1w1+d2w2+ ... + d(n-k)w(n-k)) 이다.
c1v1+c2v2+ ... + ckvk 부분을 x라고 한다면, x는 V의 원소를 표현한 식이기도 하다.
-(d1w1+d2w2+ ... + d(n-k)w(n-k)) 도 x이고, x는 V⊥의 원소를 표현한 식이 된다.
x는 V와 V⊥의 원소가 되어야하므로,
x = 0 이어야만 한다.

그 말은 즉, (c1v1+c2v2+ ... + ckvk) = 0 이고, (d1w1+d2w2+ ... + d(n-k)w(n-k)) = 0 이어야만, 두 벡터의 합이 0이 된다는 것이다.
v1, v2, ..., vk는 기저벡터로 선형독립하므로, c1, c2, ..., ck가 0이어야 (c1v1+c2v2+ ... + ckvk)를 0으로 만들 수 있다.
w1, w2, ..., w(n-k) 역시 선형독립이므로, d1, d2, ..., d(n-k)가 0이어야만 한다.
(c1v1+c2v2+ ... + ckvk) + (d1w1+d2w2+ ... + d(n-k)w(n-k)) = 0 에서
모든 상수가 0이어야만 합이 0이 될 수 있기 때문에,
v1, v2, ..., vk, w1, w2, ..., w(n-k)는 모두 선형독립이고, Rn의 기저벡터가 된다.
예전에 정리했던 내용인데,
n차원의 부분공간이 존재할 때, 그 부분공간에 속하는 n개의 선형독립 벡터가 있으며, 이 n개의 벡터 혹은 n개의 벡터 집합은 부분공간의 기저가 된다고 했다.
Rn은 n차원 부분공간이기 때문에, dim(Rn) = n이 된다.

벡터 a가 Rn의 원소라고 하자.
a = (c1v1+c2v2+ ... + ckvk) + (d1w1+d2w2+ ... + d(n-k)w(n-k)) 으로 표현할 수 있고,
(c1v1+c2v2+ ... + ckvk) 는 V의 원소 v,
(d1w1+d2w2+ ... + d(n-k)w(n-k))는 V⊥의 원소 x이다.
즉, Rn의 원소 a를 v+x(V + V⊥)의 형태로 나타낼 수 있다는 것이다.
그런데 a를 표현할 방법은 1가지로 유일할까?
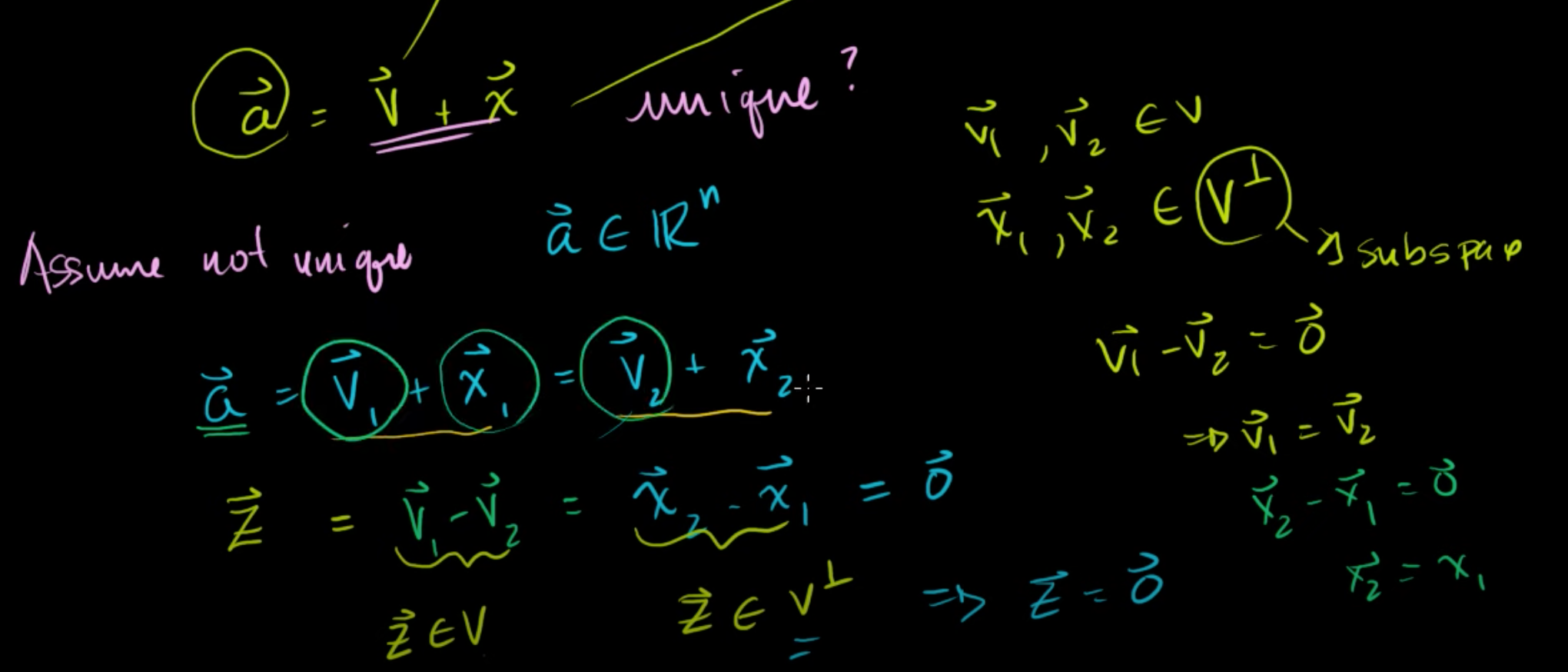
v와 x가 유일하지 않다고 가정해보자.
a = v1 + x1
a = v2 + x2 가 모두 가능하다.
v1 + x1 = v2 + x2를 정리해보면,
v1 - v2 = x2 - x1 = Z 라고 할 수 있다.
V와 V⊥은 덧셈에 닫혀있으므로,
v1 - v2 ∈ V ( = Z ∈ V)
x2 - x1 ∈ V⊥ ( = Z ∈ V⊥) 이 성립한다.
Z가 V와 V⊥의 원소이려면, Z = 0 이어야만 한다.
Z = 0 이라면,
Z = v1 - v2 = 0v1 = v2
Z = x2 - x1 = 0
x2 = x1
하지만, v1과 v2는 선형독립이기 때문에 같은 벡터가 될 수 없고, x2과 x1도 동일하다.
결론적으로 v와 x가 유일하다는 것을 알 수 있다.
따라서, Rn의 원소를 부분공간 V의 벡터와 V의 직교여공간의 벡터의 합으로 나타내는 데에는 한 가지의 고유한 방법만이 존재한다.
위의 내용을 요약하자면,
V와 V⊥의 공통의 원소는 0밖에 없다는 사실을 알아냈고,
V+V⊥이 0이 되는 유일한 해는 각각의 상수가 0일 때이며,
V와 V⊥의 기저벡터가 Rn(V+V⊥)의 기저벡터라는 사실을 알 수 있었다.
Rn의 V와 V⊥에서, Rn의 원소를 표현하는 방법은 1가지밖에 없다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 14-6. 영공간의 직교보공간 (0) | 2023.05.09 |
|---|---|
| 14-5. 직교보공간의 직교보공간 (0) | 2023.05.08 |
| 14-3. 부분공간 V와 퇴화차원의 관계 (0) | 2023.05.03 |
| 14-2. 직교보공간(직교여공간) (1) | 2023.04.28 |
| 14-1. 4대 부분공간의 직교 (0) | 2023.04.27 |