(1) 계수와 퇴화차원(Nullity)의 관계 ( = dim(V)와 dim(V⊥)의 관계)
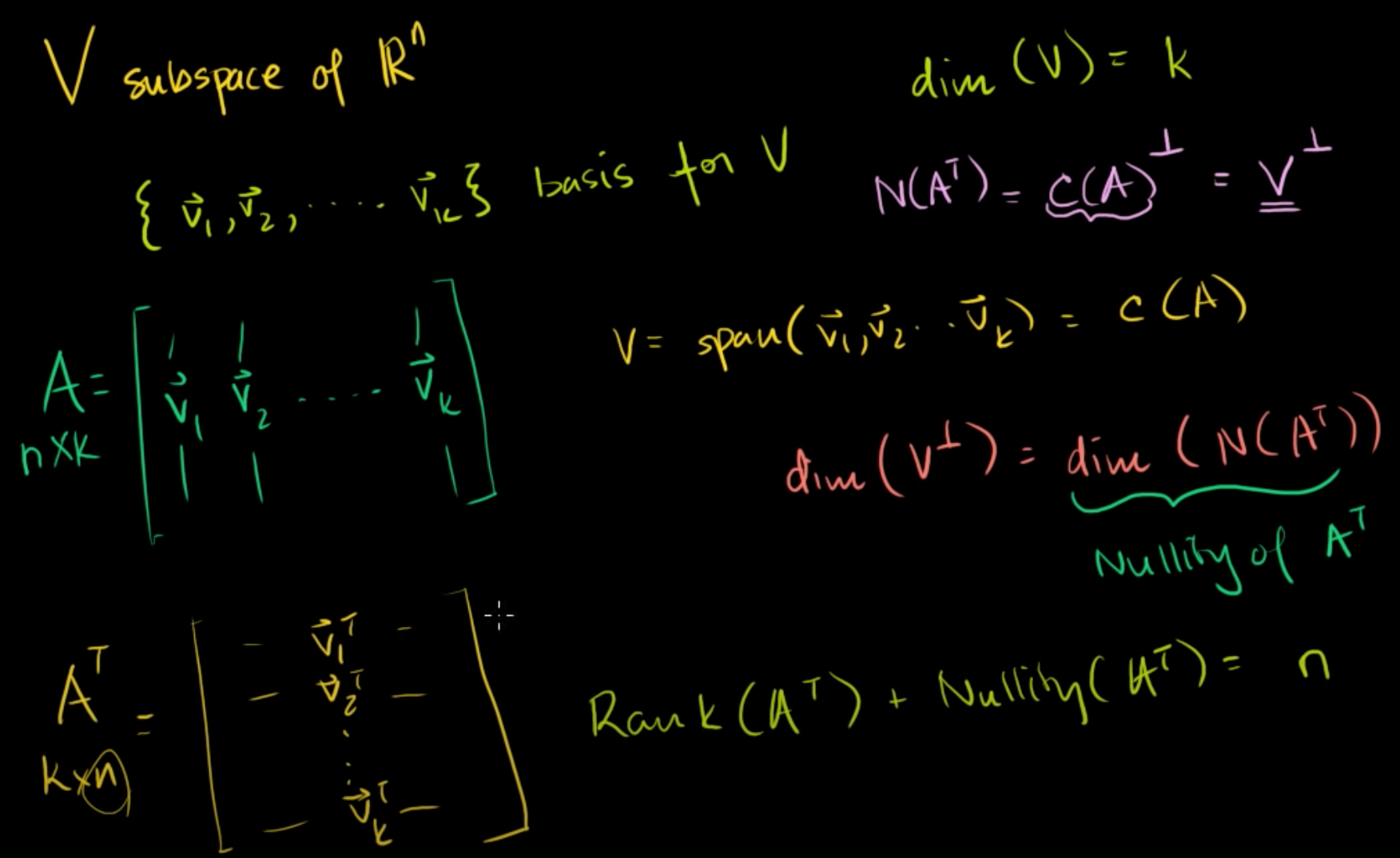
Rn의 부분공간 V가 있고, V의 기저로는 v1, v2, ..., vk가 있다고 해보자.
V의 차원은 k가 된다.
A를 기저인 v1, v2, ..., vk로 이뤄진 행렬이라고 한다면, A는 nxk의 행렬이 되게 된다.
부분공간 V는 span(v1, v2, ..., vk)로 생성할 수 있는 공간이고,
기저 v1, v2, ..., vk는 모두 선형독립이기 때문에 span(v1, v2, ..., vk)는 A의 열공간과 동일하다.
C(A)에서 직교여공간은 C(A)⊥로 표현하고, A의 전치행렬의 영공간과 동일하다. (14-2 참고)
그리고 C(A) = V라고 했기 때문에,
C(A)⊥ = N(AT) = V⊥ 가 성립한다.
그래서 V의 수직성분의 차원을 알고 싶다면, A의 좌영공간을 구하거나 열공간의 수직성분을 알면 된다.
dim(V⊥) = dim(N(AT))
dim(N(AT)) 는 AT의 nullity라고도 표현한다.
**nullity는 영공간의 차원을 의미함. (=자유변수의 개수)
AT를 구해보면, kxn의 행렬로, [v1T, v2T, ..., vkT]처럼 전치한 행벡터로 표현된다.
여기서 한 가지 알 수 있는 것은 어떤 행렬이든 Rank(AT) + Nullity(AT) = n 라는 rank와 nullity의 관계이다.

Rank(AT) = Rank(A)와 동일하기 때문에, Rank(A) + Nullity(AT) = n이 성립한다.
Rank(A) + Nullity(AT) = n 라는 것에 대해서 예시를 보면서 생각해보자.
B = [b1, b2, ..., bn] 이라고 할 때, rref에서 pivot의 개수가 Rank(A)이고 자유변수의 개수가 Nullity이다.
rref에서 free 열과 pivot 열이 아닌 열은 없기 때문에, 두 열의 개수를 합하면 rref의 열의 개수가 나온다.
따라서,
Rank(AT) + Nullity(AT) = n
Rank(A) + Nullity(AT) = n
dim(C(A)) + dim(N(AT)) = n -> B의 rank는 C(A)의 차원과 같고, Nullity(AT) = dim(N(AT))
dim(V) + dim(V⊥) = n
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 14-5. 직교보공간의 직교보공간 (0) | 2023.05.08 |
|---|---|
| 14-4. Rn의 원소를 V와 직교여공간으로 나타내기 (0) | 2023.05.04 |
| 14-2. 직교보공간(직교여공간) (1) | 2023.04.28 |
| 14-1. 4대 부분공간의 직교 (0) | 2023.04.27 |
| 13-2. 행렬과 전치행렬의 계수(Rank) (0) | 2023.04.24 |