(1) 단위행렬
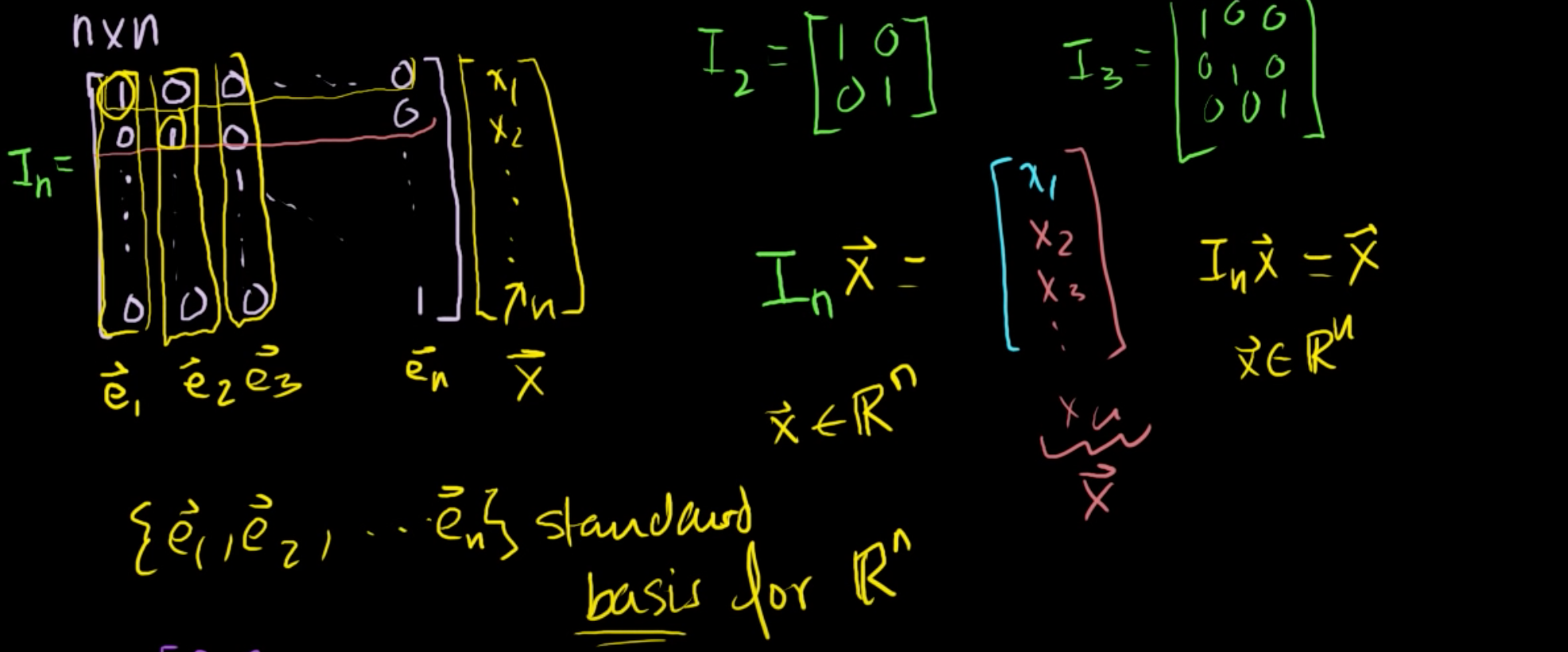
여기 n x n 단위행열 I가 존재한다고 해보자.
I2 = [1 0; 0 1], I3 = [1 0 0; 0 1 0; 0 0 1] 이 될 것이고,
단위행렬에 n개의 성분을 가지는 벡터 x를 곱한다면 결과 역시 벡터 x가 나오게 될 것이다.
그리고, 단위행렬의 각 열을 e1, e2, ..., en이라고 하면, e들은 표준기저라고 부른다. (길이가 1인 기저)
e가 기저가 되는 이유는 Rn을 생성하면서 선형독립하기 때문이다.

만약 a1, a2, 부터 an까지를 갖는 벡터를 만들고싶다고 가정해보자.
이 벡터를 만들 선형결합식은 a1 e1 + a2 e2 + ... + an en 의 합으로 표현이 된다.
(벡터의 각 성분과 단위벡터의 각 열이 곱해지면 만들 수 있다.)
이를 행렬로 표현하면 맨 우측처럼 되게 된다.
(2) 선형변환의 행렬 벡터 곱

간단하게 단위벡터에 대해서 정리해봤으니, 선형 변형에서 배운 것들을 단위벡터에 적용해보자.
벡터 x를 표준기저의 결합으로 다시 써보면, x1 e1 + x2 e2 + ... + xn en까지의 합으로 나타낼 수 있다.
x를 선형변환을 해보자.
T(x) = T(x1 e1 + x2 e2 + ... + xn en) 으로 풀어서 표현할 수 있고,
선형변환의 조건에 따라 선형변환의 합으로 표현하면,
= T(x1 e1) + T(x2 e2) + ... + T(xn en)
선형변환의 조건에 따라 스칼라를 앞으로 빼보면,
= x1T(e1) + x2T(e2) + ... + xnT(en)
= [T(e1), T(e2), ..., T(en)] [x1; x2; ...; xn]으로 표현해줄 수 있다.
결론적으로, 임의의 선형변환으로 시작했는데 행렬의 곱으로 표현되었다.
매우 간단한 계산에 불과하다.

단순히 계산한 값과 위처럼 행렬곱으로 계산한 값이 같다면 위에서 보인 증명에 문제가 없다는 것이다.
T([x1; x2]) = [x1 + 3x2; 5x2 - x1; 4x1 + x2] 라는 변환식이 있다.
이 식은 R2와 R3를 대응시키는 변환식이다.
간단하게 단위행렬 I2 = [1 0; 0 1]을 넣어보자
T(I2) = T([1; 0]) + T([0; 1])
= [1; -1; 4] + [3; 5; 1]
T(I2) = [1 3; -1 5; 4 1] 이 된다.
T([x1; x2]) = [x1 + 3x2; 5x2 - x1; 4x1 + x2] 라는 변환을 행렬과 벡터의 곱으로 표현해보자.
T([x1; x2]) = [1 3; -1 5; 4 1] [x1, x2] 로 표현할 수 있다.
이 때, [x1; x2] = [1 0; 0 1] 이므로,
[1 3; -1 5; 4 1][1 0; 0 1] = [1 3; -1 5; 4 1] 가 나온다.
위에서 계산한 결과와 행렬곱으로 표현해서 계산한 결과가 같음을 알 수 있다.
결론적으로 선형변환은 행렬의 곱으로 표현해서 계산할 수 있으며, 이렇게 하는 게 더 빠르고 정확하게 할 수 있다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 7-5. 변환의 상 im(T) (0) | 2023.03.20 |
|---|---|
| 7-4. 선분의 변환 (0) | 2023.03.18 |
| 7-2. 행렬과 벡터 곱의 선형 변환 (0) | 2023.03.16 |
| 7-1. 선형변환과 필요충분조건 (0) | 2023.03.15 |
| 6-11. 후보기저의 열공간 생성 (1) | 2023.03.14 |