(1) 벡터의 삼중곱(Triple product)
결말부터 말하면,
A×(B×C)=B(A⋅C)−C(A⋅B)
라는 식이 성립한다. (BAC CAB여서 백켑이라고도 함)
외적에서는 결합법칙이 성립하지 않기 때문에 A×(B×C) != (A×B)×C 이다.
이 식이 성립하는 과정을 아래에서 직접 계산하여 증명해보도록 하겠다.

삼중곱을 간단히하면, 내적된 값으로 다른 벡터를 상수배하여 합과 차를 한 식이 된다.
이게 무슨 말인지는 아래의 수식을 따라가면 이해할 수 있다.
벡터 a는 (a의 x성분에 단위벡터 i를 곱한 것)과( a의 y성분에 단위벡터 j와 곱한 것)과 (a의 z성분에 단위벡터 k를 곱한 것)을 다 더한 것이라고 할 수 있다.
b와 c에 대해서도 똑같이 적용할 수 있다.
b와 c의 외적을 계산하기 위해, 판별식을 세워보면 위와 같이 된다.
그리고 판별식을 풀어주면, i성분*(bycz - bzcy) - j성분*(bxcz - bzcx) + k성분*(bxcy - bycx)가 된다.
이것을 a와 외적해야 한다.
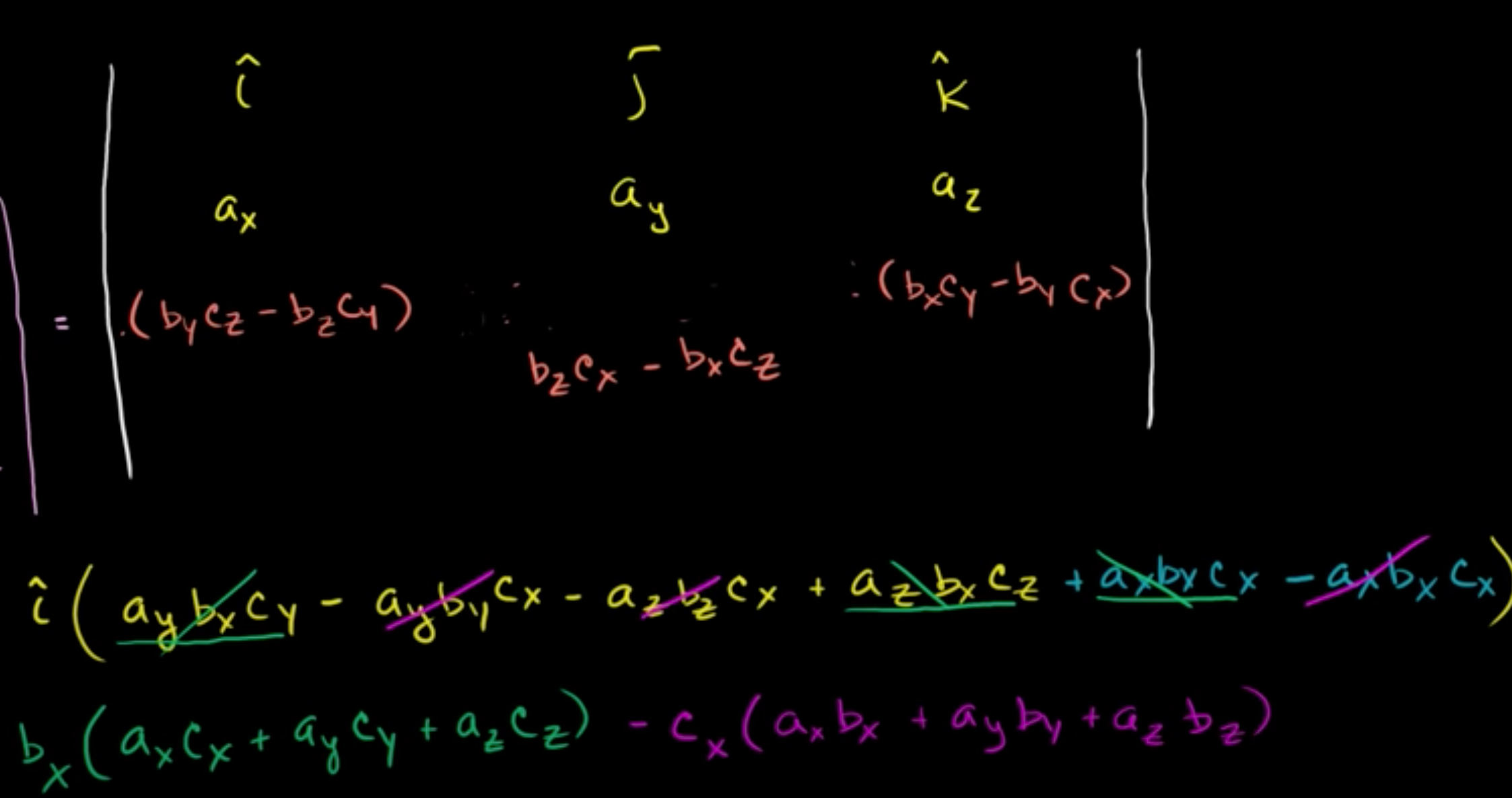
a와 i성분*(bycz - bzcy) - j성분*(bxcz - bzcx) + k성분*(bxcy - bycx)의 외적을 하기 위한, 판별식을 세워주면 위와 같이 된다.
이 식의 i성분 부분만을 풀어주면,
i성분*(ay*bxcy - ay*bycx - az*bzcx + az*bxcz) 가 되는데,
axbxcx를 더하고 axbxcx를 빼줘서 결과에는 변화가 없지만 묶어줄 수 있도록 해주겠다.
이를 bx와 -cx로 묶어주면, i성분*(bx(axcx + aycy + azcz) -cx(axbx+ayby+azbz)) 가 된다.
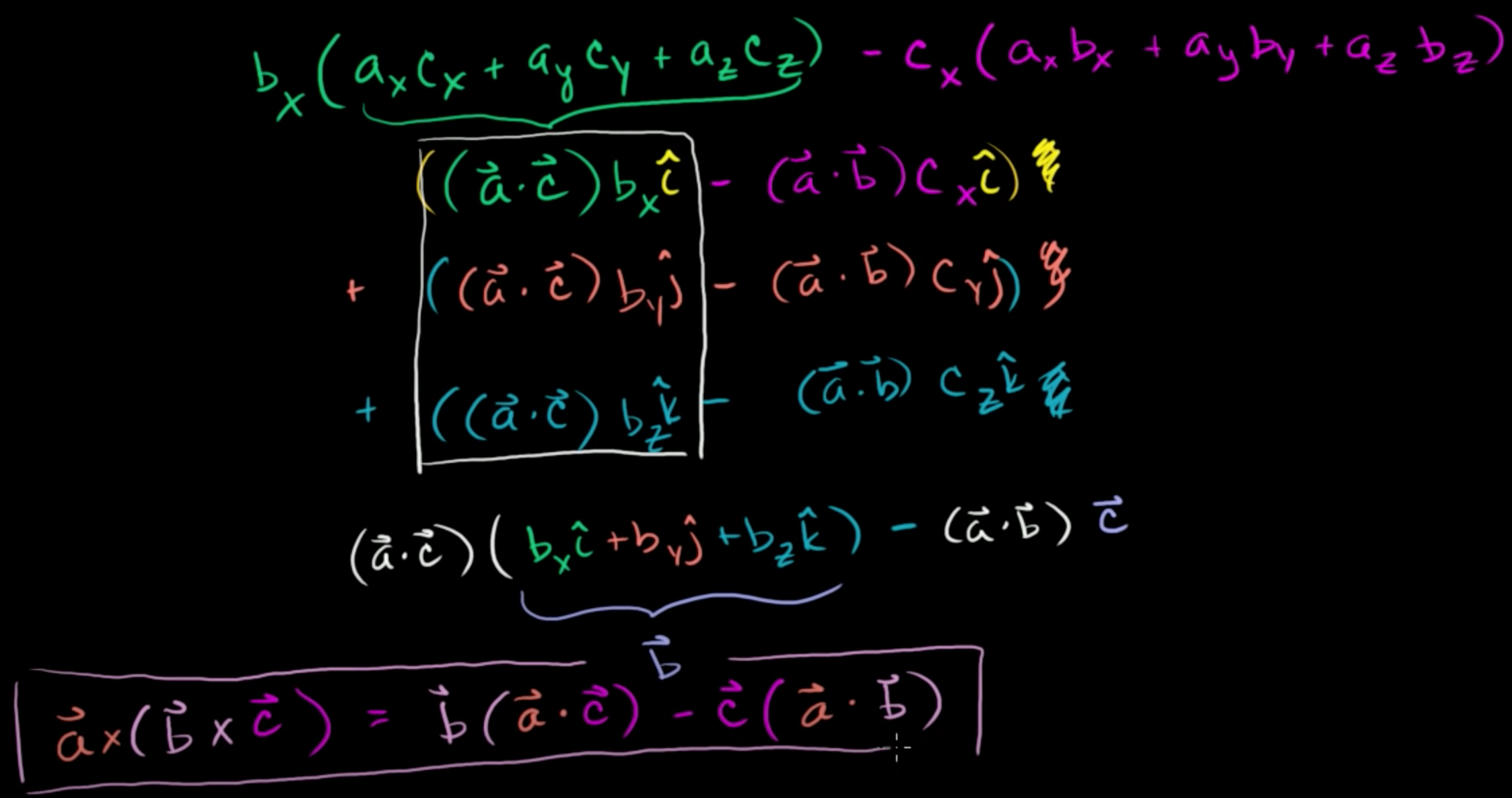
axcx + ayby + azcz는 a와 c의 내적과 동일하고, axbx+ayby+azbz는 a와 b의 내적과 동일하다.
따라서, (a · c)* bx * i성분 + (a · b)* cx * i성분 이라고 할 수 있다.
동일한 논리도, j성분과 k성분에 대한 식도 위와 같이 표현된다.
(a · c)* bx * i성분 + (a · b)* cx * i성분
+ (a · c)* by * j성분 + (a · b)* cy * j성분
+ (a · c)* bz * k성분 + (a · b)* cz * k성분
= (a · c)(bx*i + by*j + bz*k) - (a · b)(cx*i + cy*j + cz*k)
= (a · c)*b - (a · b)*c
따라서, a × (b × c) = b(a · c) - c(a · b) 가 성립한다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 4-11. 점과 평면 사이의 거리 (1) | 2023.02.24 |
|---|---|
| 4-10. 평면방정식과 법선 벡터 (0) | 2023.02.23 |
| 4-8. 외적과 내적의 비교 및 직관적 이해 (0) | 2023.02.20 |
| 4-7. 벡터의 외적과 Sin값 (0) | 2023.02.17 |
| 4-6. 벡터의 외적 (0) | 2023.02.15 |