(1) 예제1. 세 직선사이에서 최소 거리가 되는 점

위와 같이 세 직선의 방정식이 있다.
y에 대해 정리해보고, 그래프 상에 그려보면, 세 직선이 만나는 한 점은 존재하지 않는다.
Ax = b 의 해가 없는 경우이기 때문에, Ax* = b의 형태로 세 직선과의 거리가 가장 가깝게 하는 근사값을 구해볼 수 있다.
2x - y = 2
x + 2y = 1
x + y = 4
를 Ax = b의 형태로 표현해보면
[2, -1; 1, 2; 1, 1] [x, y] = [2, 1, 4] 가 되어야 한다.
ATAX* = ATb의 식을 계산해주면, X*을 구할 수 있다.
ATA = [2 1 1; -1 2 1] [2 -1; 1 2; 1 1] = [6 1; 1 6]

ATb = [2 1 1; -1 2 1][2; 1; 4] = [9; 4] 이다.
ATAX* = ATb 에 계산한 식을 대입해주면
[6 1; 1 6] X* = [9 4]
X* = [10/7; 3/7] 이 된다.
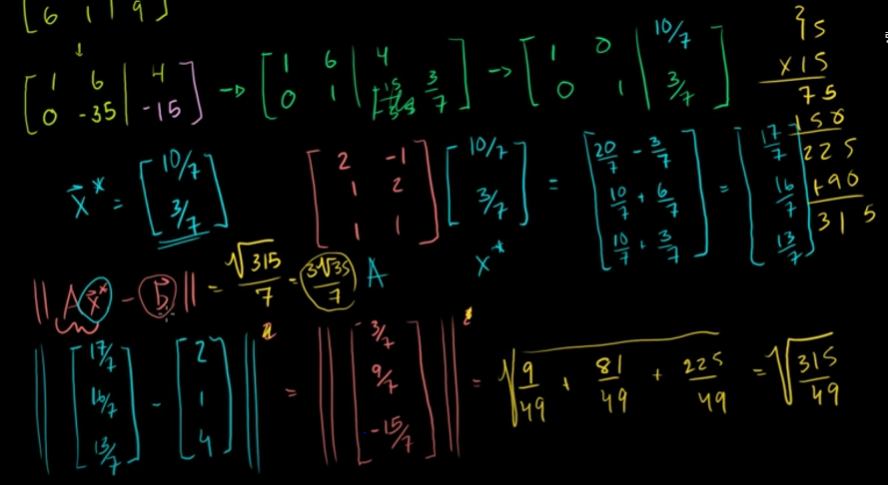
X* = [10/7; 3/7] 이므로,
AX* = [17/7, 16/7, 13/7] 이 된다.
||Ax* - b|| = ||[3/7, 9/7, -15/7]||
따라서, 제곱의 최소값은 3√35/7
(2) 예제2. 점들을 지나는 직선
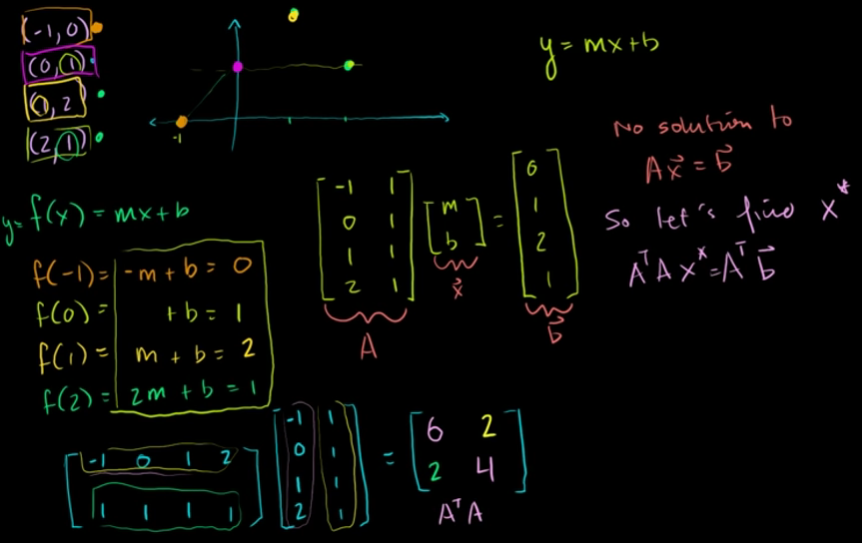
네 점 (-1, 0), (0, 1), (1, 2), (2, 1)이 있다.
네 점을 지나는 y = mx + b는 사실 없다.
그러면 네 점과의 거리가 최소가 되는 직선을 구해보자.
Ax = b의 형태로 표현해보면,
[-1, 1; 0, 1; 1, 1; 2, 1;] [m, b] = [0, 1, 2, 1]
ATAX* = ATb 의 형태로 계산해보자.
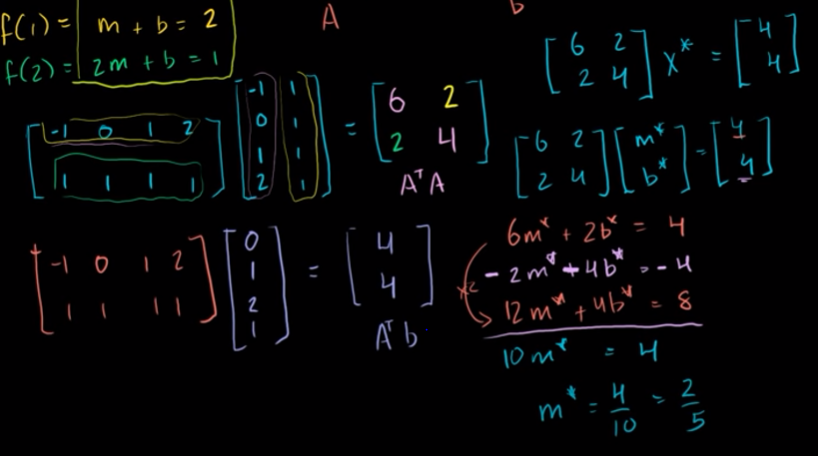
[6, 2; 2, 4] [m*, b*] = [4, 4]
m* = 2/5

b* = 4/5
y* = 2/5x + 4/5
이 직선의 방정식일 때, 네 점과의 거리가 가장 짧다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 16-2. 기저변환행렬 (0) | 2023.05.29 |
|---|---|
| 16-1. 기저에 대한 좌표 (0) | 2023.05.28 |
| 15-5. 정사영을 활용하여 최소 제곱이 되는 근사값 구하기 (0) | 2023.05.26 |
| 15-4. 정사영은 부분공간에 가장 가까운 벡터 (0) | 2023.05.25 |
| 15-3. 부분공간에 대한 정사영은 선형변환 (0) | 2023.05.22 |