반응형
(1) 원상이란? (Preimage)

원소들을 집합 X에서 집합 Y로 대응시키는 변환 T가 있다.
집합 X는 T의 정의역이고, 집합 X에 대응하는 집합 Y는 공역이다.
T는 집합 X의 아무 원소나 대응시켰을 때 집합 Y의 원소로 바뀌는 변환이다.
T의 부분집합(subset) A를 초록색, A의 상을 파란색으로 그려보면 위와 같이 된다.
이 때, T(A)를 T에 대한 A의 상이라고 표현했다.
이번에 우리가 알고 싶은 것은 T(A)만을 알 때, A를 구할 수 있는가이다.
오른쪽에 새로운 그림을 그려서, 집합 Y와 집합 Y의 부분집합인 S가 있다.
그러면 집합 X의 어떤 부분집합이 집합 S에 대응할까? (부분집합 S로 변환되는 벡터의 집합을 구해보자)
주의해야할 점은 집합 S의 모든 원소들이 반드시 대응하는 것은 아니라는 것이다.
예를 들어, 집합 S의 어떤 원소는 변환 T에 의해서 X의 어떤 원소로도 만들 수 없을 수도 있기 때문이다.
하지만, 빨간색으로 그린 집합의 모든 원소들은 집합 S의 무언가에 대응한다.
이 빨간색의 집합을 표기할 때, 집합 S의 역함수 T라고 부르지만 이것은 T에 있는 집합 S의 원상과 같다.
집합 S의 원상의 상은 무엇일까?
원상의 상 모두는 집합 S 안에 있게 되므로 따라서 집합 S 안으로 대응하지만 반드시 집합 S의 모든 것에 대응할 필요는 없다.
따라서 이것은 집합 S의 어떤 부분집합이 될 것이다.
(2) 원상의 예제

예시를 들어보자.
선형변환 T는 R2에서 R2로 변환해주는 [1, 3; 2, 6]이라고 해보자.
그리고 우리가 알고 있는 상 S는 {[0; 0], [1; 2]}이다.
이 때, T에 대한 S의 원상인 T'(S)를 구해보자.
그림으로 그려보면 R2의 [1 2]와 [0 0]으로 사상(mapping)되는 노란색 T'(S)를 구하는 것이다.
T(x)는 Ax라는 변환으로 생각할 수 있고, Ax = [0 0] or Ax = [1 2]를 성립하는 x의 집합이 원상이 된다.

이를 첨가행렬로 표현해서 풀어보도록 하자.
[ 1 3; 2 6][x1; x2] = [0; 0]
이를 기약행사다리꼴 행렬로 풀어주면,
[1 3 | 0
0 0 | 0] 이다.
[ 1 3; 2 6][x1; x2] = [1; 2]
이를 기약행사다리꼴 행렬로 풀어주면,
[1 3 | 1
0 0 | 0] 이다.
이제 이것들을 만족 시키는 x1과 x2를 어떻게 찾을까?
첫번째 열이 피벗열이고 두번째 열은 자유열이기 때문에, x1은 피벗변수이고 x2는 자유변수이다.
자유변수 x2를 t로 표현해보면,
첫번째 행렬은
x1 + 3x2 = 0
x1 + 3t = 0
x1 = -3t
x2 = t
두번째 행렬은
x1 + 3x2 = 1
x1 + 3t = 1
x1 = -3t + 1
x2 = t
이다.
따라서,
[x1, x2] = t[-3, 1] (t는 실수)
[x1, x2] = [1, 0] + t[-3, 1] (t는 실수) 가 된다.
이를 그래프 상으로 표현해보자.
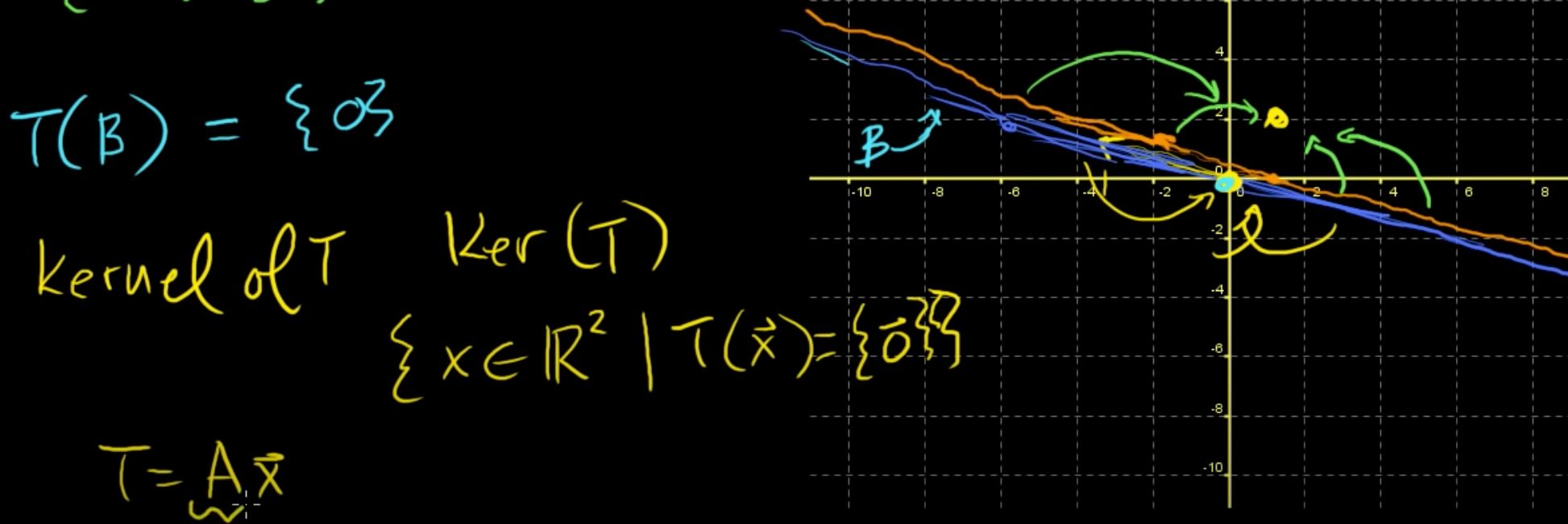
첫번째 식은 파란색의 원점을 지나는 직선
두번째 식은 주황색의 직선이 되고,
두 직선은 똑같은 기울기를 가지며 평행이동을 한 선이다.
여기서 파란색 직선 상의 모든 점들은 T를 통해 (0, 0)으로 사상(mapping)되며,
주황색 직선 상의 모든 점들은 T를 통해 (1, 2)로 사상된다.
여기서 (0, 0)으로 사상되는 파란색 직선은 특별한 이름이 있다.
T의 핵, 커널, Ker(T)라고 불린다.
커널이라는 의미는 변환이 영벡터가 되는 정의역에 있는 모든 벡터들을 뜻한다.
T의 핵은 (0,0)으로 사상되는 벡터 x들이기 때문에, A의 영공간이라고도 할 수 있다.
반응형
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 8-1. 선형변환(스케일 변환 행렬, 반사 변환 행렬) (0) | 2023.03.23 |
|---|---|
| 7-7. 선형변환의 합, 스칼라 곱 (0) | 2023.03.22 |
| 7-5. 변환의 상 im(T) (0) | 2023.03.20 |
| 7-4. 선분의 변환 (0) | 2023.03.18 |
| 7-3. 선형변환의 행렬 벡터 곱 (0) | 2023.03.17 |