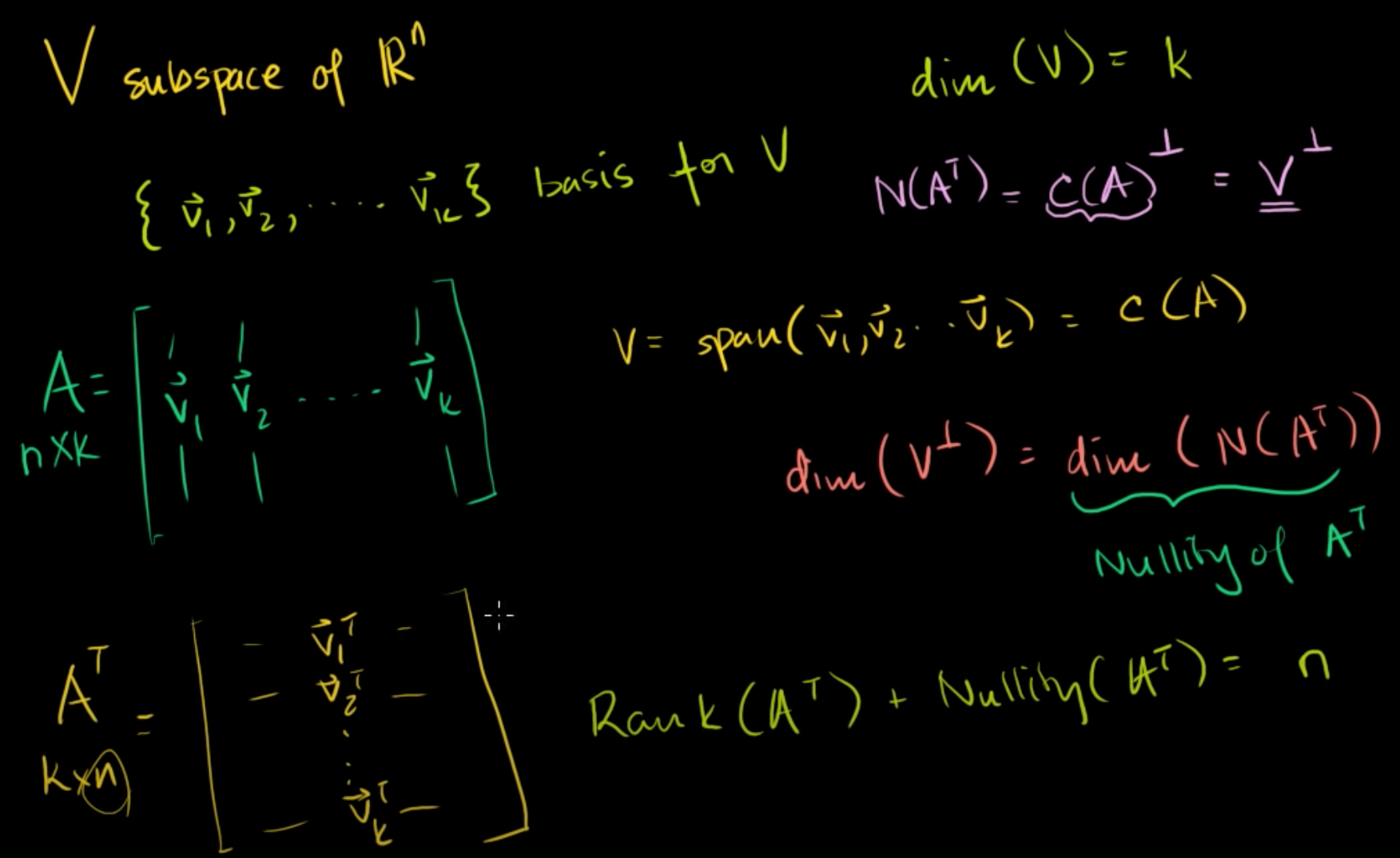SInce 20180106

(1) 영공간의 직교보공간(직교여공간) 행렬 A가 있다. 이전 글에서 행공간은 열공간의 전치와 같다고 했다. 따라서, C(AT) = R(A)라고 할 수 있따. 그리고 C(AT)⊥ = N(A) 와 같다고 했다. 또한, C(A)⊥ = N(AT) (열공간의 직교여공간은 좌영공간과 같다) 14-5에서 다룬 것처럼 ⊥의 ⊥는 원래의 행렬로 돌아오기 때문에, 영공간의 직교여공간은 어떻게 될까? N(A)⊥ = (C(AT)⊥)⊥ = C(AT). 즉, A 영공간의 직교보공간은 A의 전치의 열공간과 같다. 좌영공간의 직교여공간은 어떻게 될까? N(AT)⊥ = (C(A)⊥)⊥ = C(A) 즉, A 좌영공간의 직교보공간은 A의 열공간과 같다. 정리하자면, N(A) = R(A)⊥ 이고, R(A) = N(A)⊥ 이다. N(AT)..

(1) V와 V의 직교여공간으로 Rn 표현하기 Rn의 부분집합은 부분공간 V가 있고, V의 직교여공간인 V⊥가 있고 이것 또한 Rn의 부분집합이다. 앞에서 정리한 것처럼 dim(V) + dim(V⊥) = n이다. 두 부분공간이 공통으로 가지는 벡터가 존재할까? x라는 벡터가 V와 V⊥의 원소라고 가정해보자. 둘이 직교하기 때문에 V에 속하는 모든 v에 대해서 x·v = 0 이고, x·x = 0 역시 성립한다. 자기 자신과의 내적은 길이의 제곱과 같기 때문에, ||x||²=0 이라는 의미이고, 이는 x = 0 일때만 성립한다. 따라서, V와 V⊥의 교집합 원소는 0이고, 이를 그림으로 그려보면 위와 같이 된다. dim(V) = k 라고 하면, dim(V⊥) = n-k 가 된다. 차원은 기저에 필요한 선형독..

(1) 계수와 퇴화차원(Nullity)의 관계 ( = dim(V)와 dim(V⊥)의 관계) Rn의 부분공간 V가 있고, V의 기저로는 v1, v2, ..., vk가 있다고 해보자. V의 차원은 k가 된다. A를 기저인 v1, v2, ..., vk로 이뤄진 행렬이라고 한다면, A는 nxk의 행렬이 되게 된다. 부분공간 V는 span(v1, v2, ..., vk)로 생성할 수 있는 공간이고, 기저 v1, v2, ..., vk는 모두 선형독립이기 때문에 span(v1, v2, ..., vk)는 A의 열공간과 동일하다. C(A)에서 직교여공간은 C(A)⊥로 표현하고, A의 전치행렬의 영공간과 동일하다. (14-2 참고) 그리고 C(A) = V라고 했기 때문에, C(A)⊥ = N(AT) = V⊥ 가 성립한다. 그..

(1) 직교보공간(직교여공간) Rn의 부분공간 V가 있다고 하자. 이 부분공간 V의 부분여공간을 V⊥라고 하자. (⊥는 직각이라는 뜻의 perpendicular에서 따온 perp라고 읽는다.) V⊥를 정의하자면, 부분공간 V의 모든 원소 v에 대해 x∙v = 0을 만족하는 x의 집합이다. 근본적으로 말하면, 부분공간의 모든 원소와 직교하는 벡터들이 원소로 있는 집합을 직교여공간이라고 한다. V⊥이 부분공간인지 확인해보자. 부분공간이 되기 위해서는 덧셈과 스칼라곱에 닫혀있어야한다. a, b가 V⊥의 원소이고 v가 V의 원소라면, a∙v = 0 & b∙v = 0 이고, (a+b)∙v =0 (덧셈에 닫혀있다.) ca∙v = c(a∙v) = 0 (스칼라 곱에 닫혀있다) 따라서, V⊥는 부분공간이다. 이는 V⊥에..