SInce 20180106

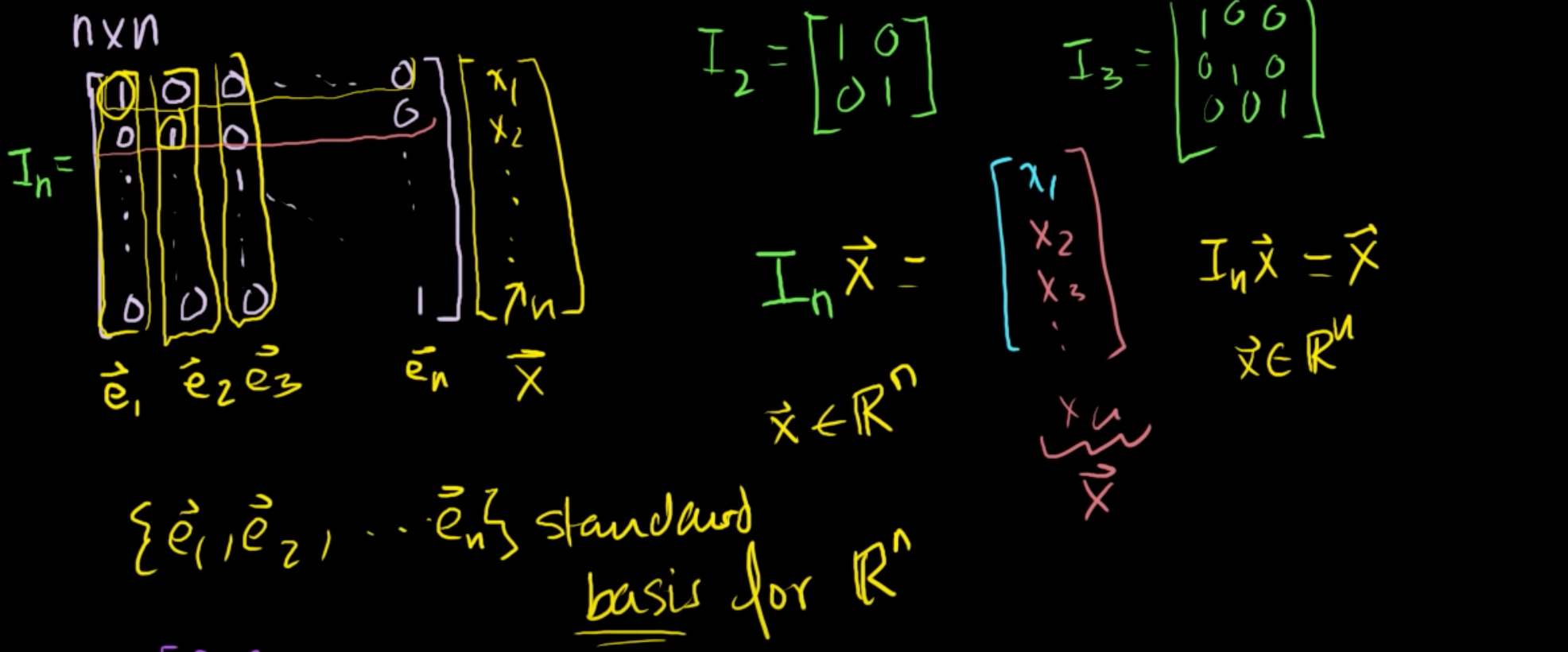
(1) 단위행렬 여기 n x n 단위행열 I가 존재한다고 해보자. I2 = [1 0; 0 1], I3 = [1 0 0; 0 1 0; 0 0 1] 이 될 것이고, 단위행렬에 n개의 성분을 가지는 벡터 x를 곱한다면 결과 역시 벡터 x가 나오게 될 것이다. 그리고, 단위행렬의 각 열을 e1, e2, ..., en이라고 하면, e들은 표준기저라고 부른다. (길이가 1인 기저) e가 기저가 되는 이유는 Rn을 생성하면서 선형독립하기 때문이다. 만약 a1, a2, 부터 an까지를 갖는 벡터를 만들고싶다고 가정해보자. 이 벡터를 만들 선형결합식은 a1 e1 + a2 e2 + ... + an en 의 합으로 표현이 된다. (벡터의 각 성분과 단위벡터의 각 열이 곱해지면 만들 수 있다.) 이를 행렬로 표현하면 맨 우측..

(1) 행렬과 벡터의 곱, 그리고 선형 변환 행렬을 벡터와의 내적으로 변환하는 과정을 보여주고, 이런 변환이 선형변환인지 알아보도록 하자. m x n 행렬 A는 열벡터 v1, v2부터 vn으로 표현할 수 있다. 이 때, 변환 T는 Rn에서 Rm으로 가는 변환이라고 하고, 벡터 x가 입력되면 행렬 A를 내적하여 나온 값으로 변환해준다고 해보자. 조금 생소해보일 수도 있지만, 이 역시 변환의 일종이니 익숙해지도록 노력해보자. T(x) = Ax 이고, 결과는 Rm 상에 존재한다. Ax = [v1, v2, ..., vn] [x1; x2; ... xn] 이라는 행렬과 벡터의 내적으로 표현할 수 있고, 이를 풀어보면, v1x1 + v2x2 + .. + vnxn 이다. 이 결과는 Rm 상에 존재하며, v1, v2, ..

(1) 선형변환 (Linear Transformation) 함수는 쉽게 말하면 하나의 값을 다른 값으로 변환해주는 식이다. 변환에서도 특별한 종류인 선형변환에 대해 알아보겠다. 선형변환은 Rn에서 Rm으로 변환해주는 것이고, 무엇인가가 선형변환이라는 것은 필요충분조건 2가지를 만족한다는 것이다. 조건 1) 두 벡터의 합 벡터의 변환 결과는 벡터 각각을 선형변환하여 더한 것과 같다. 조건 2) 벡터에 스칼라나 실수를 곱한 것을 변환한 결과는 벡터를 변환한 것에 스칼라배한 것과 같다. 이러한 규칙으로 선형변환인지 아닌지 판별할 수 있는지 알아보자. 변환 T는 (x₁, x₂)를 (x₁+x₂, 3x₁)으로 바꿔주는 함수가 있다고 가정하자. (R²에서 R²로 변환) T가 선형변환인지 아닌지 판단해보자. 조건 1)..