(1) 회전변환은 선형변환인가?
이 글로 각도 θ로 회전변환을 하는 변환도 선형변환인지 알아보고, 어떻게 선형변환 행렬을 만들 수 있는지 알아보자.
R2에서 R2로 회전하는 변환 Rotθ가 있다.
이 변환은 벡터 x를 반시계방향으로 θ만큼 회전시키는 변환이다.
이게 선형변환인지 알기 위해서는 두 가지 조건이 성립하는지 체크해보면 된다.
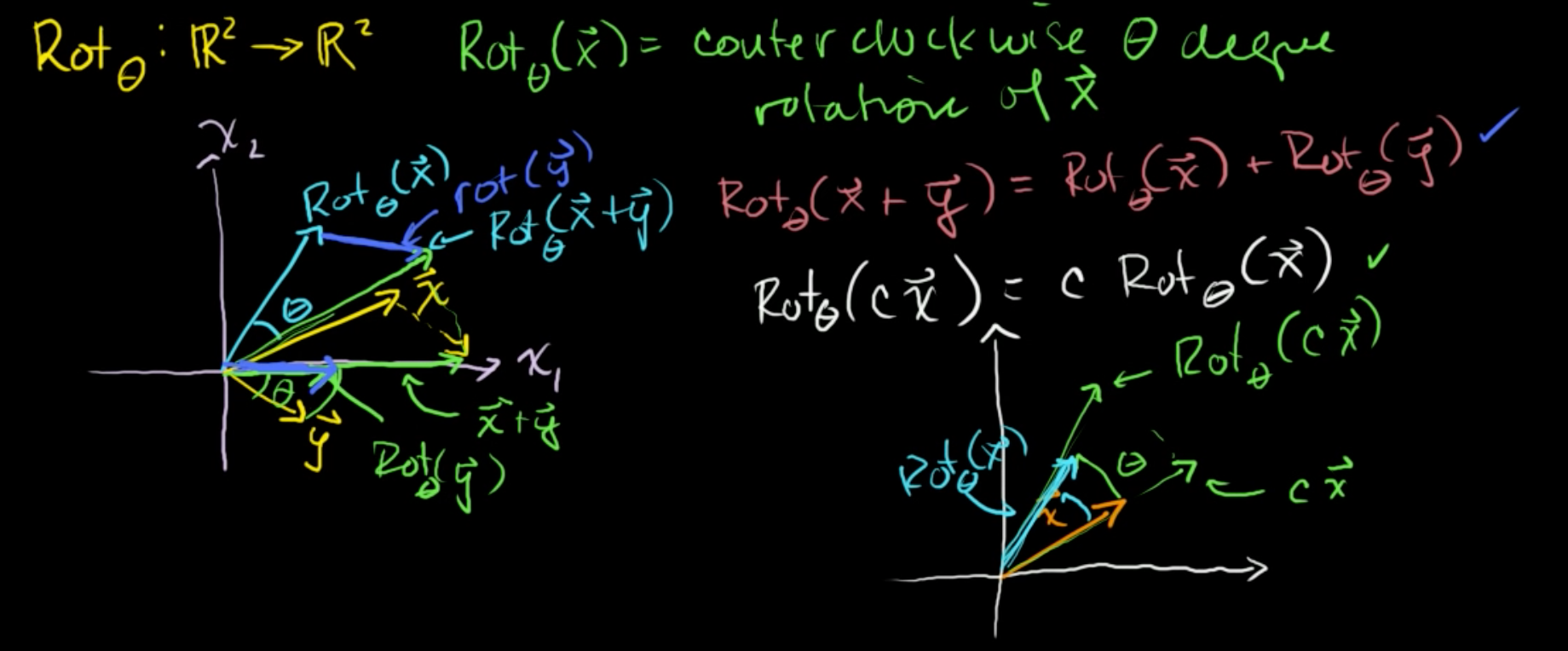
1) Rotθ(x+y) = Rotθ(x) + Rotθ(y) 인가?
왼쪽처럼 2차원 좌표를 그리고, 노란색으로 벡터 x, y를 그리고 초록색으로 x+y를 표현했다.
반시계방향으로 θ만큼 회전한 Rotθ(x)를 하늘색, Rotθ(y)를 파란색으로 나타내봤다.
x+y를 θ만큼 회전한 Rotθ(x+y)도 하늘색으로 그려보면, Rotθ(x) + Rotθ(y)의 값과 일치한다.
따라서, Rotθ(x+y) = Rotθ(x) + Rotθ(y) 이다.
2) Rotθ(cx) = cRotθ(x) 인가?
x를 주황색, cx를 연두색으로 그려봤다.
각각의 벡터를 θ만큼 회전한
Rotθ(x)를 하늘색, Rotθ(cx)를 연두색으로 그려봤다.
Rotθ(cx)는 Rotθ(x)를 c배한 것과 동일하다.
따라서, Rotθ(cx) = cRotθ(x) 이다.
두 가지 조건이 성립하기 때문에 회전변환은 선형변환이다.
(2) 회전변환의 A 행렬 구하기

그럼 이 변환을 보여줄 행렬을 한번 만들어 보자,
R2에 속한 벡터 x를 R2로 회전변환하기 때문에, Rotθ(x) = Ax에서 A는 2×2 행렬로 정의된다.
표준기저 I = [1 0; 0 1]에서 각 열벡터를 e1, e2라고 하자.
그렇다면 A = [ Rotθ[1 0] , Rotθ[0 1] ] 이라고 할 수 있다.
Rotθ[1 0]의 값을 구해보자.
2차원 좌표 상에 분홍색으로 e1을 그리고, 이를 회전한 Rotθ(e1)을 연두색으로 그렸다.
두 선을 활용하여 빗변이 1인 직각삼각형을 그리기 위해, 높이로 분홍색 선을 그었다.
삼각함수에 의해서 cosθ = 밑변 / 빗변, sinθ = 높이 / 빗변이다.
따라서, Rotθ(e1) = [ cosθ / 1, sinθ/ 1] = [ cosθ , sinθ ]이다.
똑같이 Rotθ[0 1]의 값을 구해보자.
2차원 좌표 상에 노란색으로 e2을 그리고, 이를 회전한 Rotθ(e2)을 하늘색으로 그렸다.
삼각함수에 의해서 , Rotθ(e2) = [ -sinθ/ 1, cosθ / 1] = [ -sinθ , cosθ ] 이다.
따라서, A = [cosθ , -sinθ; sinθ cosθ ] 이다.
2차원 공간에서 θ만큼 반시계방향으로 회전하는 Rotθ(x) = [cosθ , -sinθ; sinθ cosθ ] [x1, x2]
예를 들어 θ가 45도라면, Rot45(x) = [cos45 , -sin45; sin45 cos45 ] [x1, x2]
= [√2/2 , -√2/2; √2/2 √2/2 ] [x1, x2]
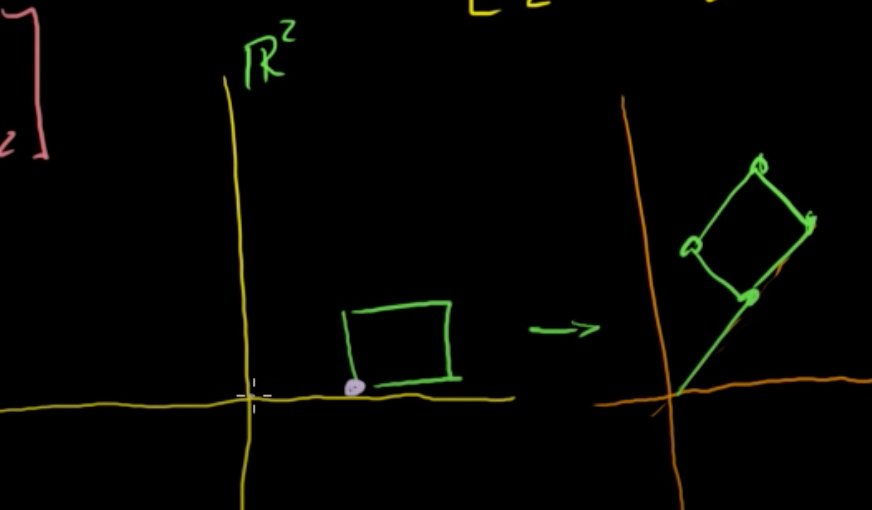
이를 활용하여, 위와 같이 사각형이 있을 때 이동한 각도를 알면 회전된 사각형을 쉽게 구할 수 있다.
'선형대수(Linear Algebra)' 카테고리의 다른 글
| 8-4. 단위벡터(Unit Vector) (0) | 2023.03.28 |
|---|---|
| 8-3. 선형변환(R3에서의 회전) (0) | 2023.03.27 |
| 8-1. 선형변환(스케일 변환 행렬, 반사 변환 행렬) (0) | 2023.03.23 |
| 7-7. 선형변환의 합, 스칼라 곱 (0) | 2023.03.22 |
| 7-6. 변환의 원상(preimage)과 핵(kernel) (0) | 2023.03.21 |