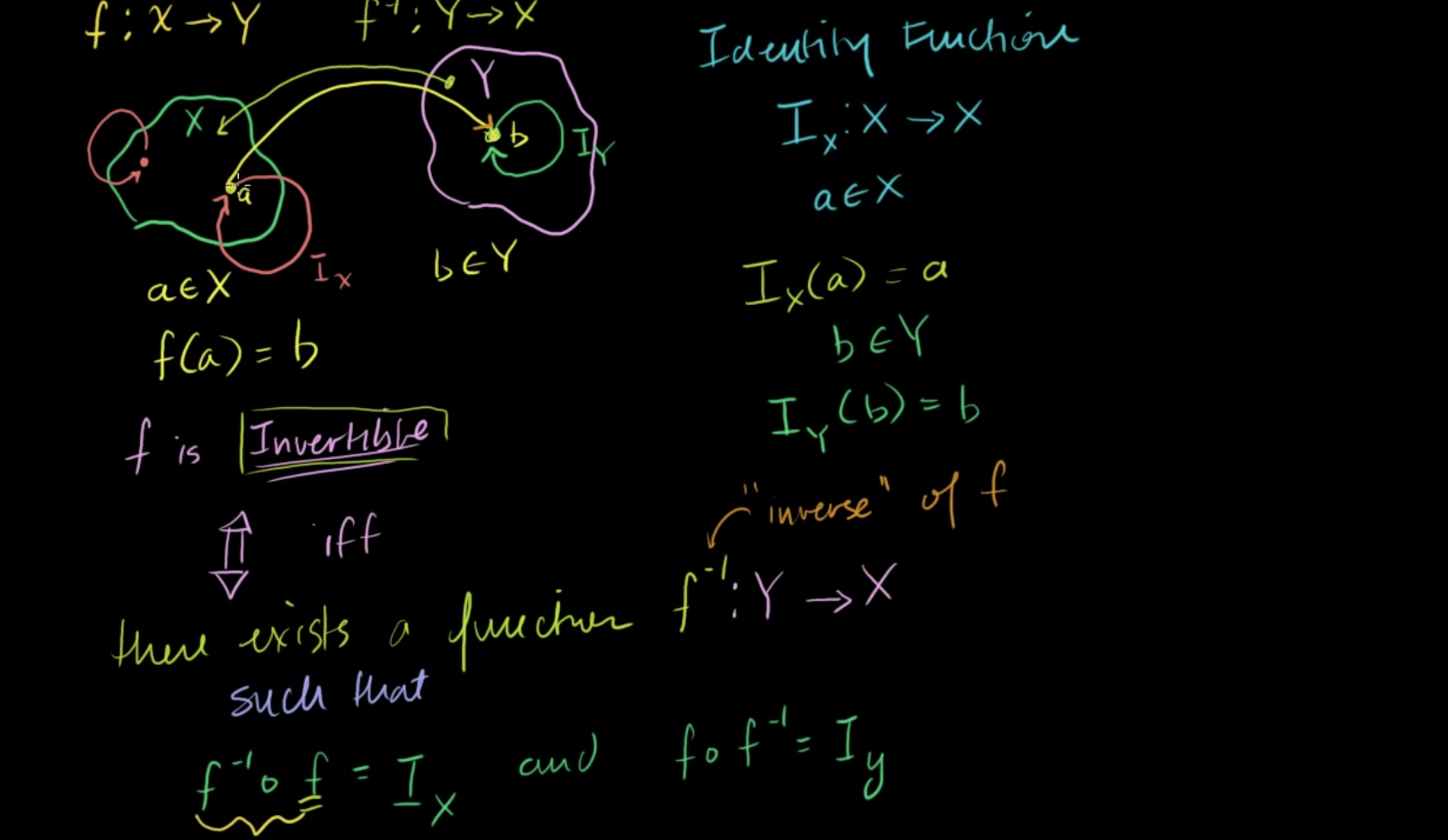(1) 역함수의 정의 어떤 함수 f를 f : Χ -> Υ 라고 정의하고, f(^-1) : Y -> X라고 정의해보자. (역함수) a가 집합 X의 원소이고, b가 집합 Y의 원소일 때, f(a) = b 이고, f^-1(b) = a가 성립한다. 항등함수(대문자 Ι)란 Ι : X -> X 이고, I(a) = a가 되는 함수이다. 즉, 임의의 원소 a에 항등함수를 적용하면 결과값이 똑같이 a가 나온다는 것이다. 그림으로 표현해보면, 원과 같은 형태가 나오게 된다. 만약 f가 가역적(invertible)이라면, f(^-1)이 존재한다는 것과 필요충분조건이다. 필요충분조건이라는 것은 ( 또는 iff)로 나타낸다. (명제가 참이고, 역도 참이라는 뜻) "f의 역함수가 존재할 때, f는 가역적이다."라고 할 수 있다...