2-1. 신경망의 기본 구성 요소 - 퍼셉트론과 활성화함수

1. 퍼셉트론

 

퍼셉트론은 가장 간단한 신경망으로 입력, 연산, 출력으로 이뤄진다.

 

퍼셉트론은 위 그림처럼 다수의 입력을 받고, 해당 입력에 f(wx + b) 연산을 진행하고, 일반적으로 비선형 함수인 활성화 함수를 거쳐, y hat값을 구하는 과정이다.

 

즉, 퍼셉트론은 선형함수와 비선형함수의 조합이다.

 

선형함수인 wx + b 연산을 affine transformation(아핀 변환)이라고도 부른다.

 

 

2. 활성화 함수

(1) 시그모이드

신경망 분야의 초창기부터 사용한 활성화 함수로, 임의의 실수값을 받아서 0과 1 사이의 범위로 압축한다.

 

식은 다음과 같으며, 

그래프는 다음과 같다.

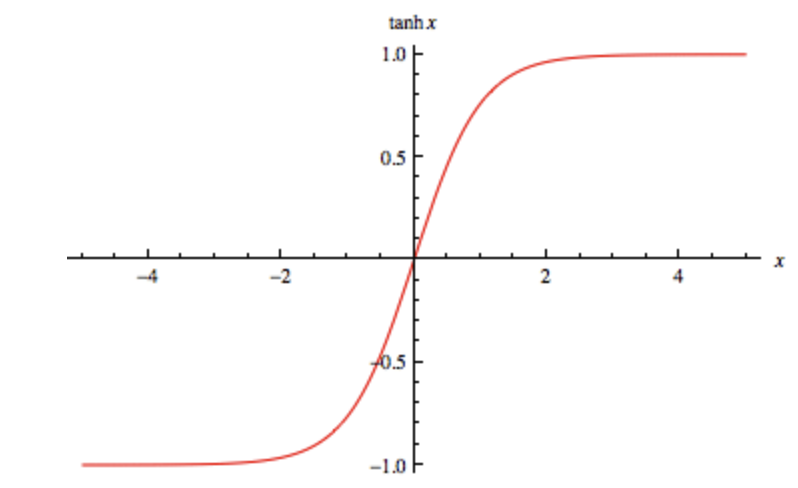
그래프에서 볼 수 있다시피, 입력이 얼마나 큰 값이 들어오던 상관없이 0과 1로 수렴하기 때문에 매우 극단적인 출력을 만들곤 한다.

 

장점으로는

- 출력 범위가 0~1이기 때문에, 이진분류에 사용하기 좋다는 점

- 기울기가 급격하게 변해서 미분값이 발산하는 기울기 폭주(Gradient Exploding)이 발생하지 않는다

 

단점으로는

- 입력크기가 아무리 크더라도, 출력되는 값의 범위가 매우 좁기 때문에 경사하강법 수행 시에 범위가 너무 좁아 0에 수렴하는 기울기 소실(Gradient Vanishing)이 발생한다.

- 학습속도가 저하된다.

 

한마디로 요약하면, 출력값이 너무 작아 제대로 학습이 진행되지 않고 시간만 걸리기 때문에 hidden layer에서는 사용하지 말고 (이진분류 문제에서의) 출력층에서만 사용하라는 것이다.

 

 

(2) 하이퍼볼릭 탄젠트

시그모이드 함수의 발전형이라고 할 수 있다.

 

식은 다음과 같으며, 

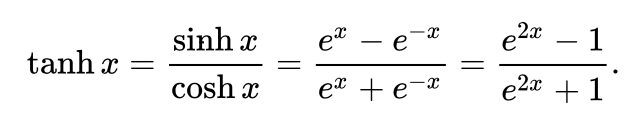
그래프는 다음과 같다.

 

tahn(x) = (1-e^-2x) / (1 + e^-2x) = ( 2 - (1+e^-2x) ) / (1+e^-2x) = 2 / (1+e^-2x) -1 

sig(x) = 1 / (1+e^-x)

이기 때문에

tahn(x) = 2 * sig(2x) -1 로 표현할 수 있다.

즉, 하이퍼볼릭 탄젠트는 시그모이드 함수의 선형 변환이다.

 

위의 식과 그래프를 보면 시그모이드와 하이퍼볼릭 탄젠트의 차이가 뭔지 알 수 있다.

 

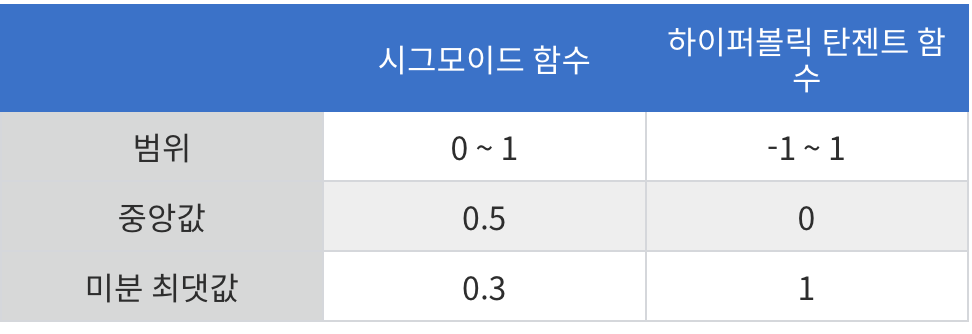
장점으로는

- 중앙값이 0이기 때문에, 경사하강법 사용 시 시그모이드 함수에서 발생하는 편향 이동이 발생하지 않는다. 

- 시그모이드 함수보다 범위가 넓기 때문에 출력값의 변화폭이 더 크고, 기울기 소실(Gradient Vanishing) 현상이 적은 편이다.

- 기울기가 양수, 음수 둘 다 나올 수 있기 때문에 시그모이드 함수보다 학습 효율성이 뛰어나다.

 

단점으로는

- 기울기 소실 현상이 적을 뿐이지 아예 없는 것은 아니다. 따라서, 조심히 사용해야 한다.

 

 

(3) 렐루

렐루는 매우 간단한 식이지만, 놀랍게도 최근에 등장한 수식이다.

 

식은 다음과 같으며,

그래프는 다음과 같다.

 

간단하게, 양수면 자기 자신을 반환하고 음수면 0을 반환한다.

 

장점으로는

- 값이 특정 양수 값에 수렴하지 않기 때문에, 기울기 소실이 발생하지 않는다.

- 속도가 매우 빠르다. (수식이 매우 간단하기 때문)

 

단점으로는

- 음수 값은 0으로 반환하다보니, 입력값이 음수인 경우 기울기도 모두 0으로 나오게 된다.

- 이 경우에 가중치 업데이트가 안되는 현상이 발생할 수도 있다.

- 가중치가 업데이트 되는 중에 가중치의 합이 0이 되어버리면, ReLu는 0을 반환하기 때문에 해당 뉴런은 무조건 0만 반환하는 죽은 뉴런(Dead Neuron)이 발생할 수 있다.

- 0에서 미분이 불가능하다. (하지만 0에 걸릴 확률이 적으니, 그냥 무시하고 사용한다)

- 출력값이 모두 0 아니면 양수이기 때문에, 시그모이드함수처럼 w 업데이트 시 지그재그로 최적의 가중치를 찾아가는 지그재그 현상이 발생한다.

 

해당 문제점을 해결하기 위해서, LeakyReLudhk PReLu와 같은 방법론이 개발되었다.

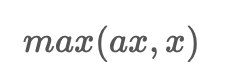
와 같은 식으로 개선하여, 음수에서도 출력값이 0이 아닌 수를 출력하게 했지만, 음수에서도 선형성이 생기게 되어 복잡한 분류에서 성능이 떨어지는 문제가 발생한다. 

 

따라서, 위와 같은 활성화함수는 음수가 아주 중요한 상황에서만 제한적으로 사용하는 것을 추천한다.

 

기본적으로 ReLu를 사용하고, 성능 개선 시 위의 활성화 함수로 바꿔가면서 실험해보면 좋다.

 

 

(4) 소프트맥스

시그모이드 함수처럼 신경망 유닛의 출력을 0과 1 사이로 압축하지만, 모든 출력의 합으로 각 출력을 나누어 n 개의 클래스에 대한 이산 확률 분포를 만든다.

 

식은 다음과 같다. 

 

장점으로는

- 지수함수이기 때문에 입력된 인자들의 대소 관계는 변하지 않으면서도, 작은 값의 차이도 확실히 구별될 정도로 커진다.

 

단점으로는

- 지수함수이기 때문에 입력값이 너무 크면, 연산이 불가능한 오버플로 문제가 발생할 수도 있다.

 

소프트맥스는 주로 확률 기반의 목적 함수인 범주형 크로스 엔트로피와 함께 사용된다.